【疫学専門家監修】選択バイアスを徹底解説 - 消えた患者が結果を歪める？ - ゼロから学ぶ因果推論 vol.14

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに

論文のLimitationとしてよく出てくる「選択バイアス」の本当の意味と、その怖さをご存じですか？

選択バイアスとは、研究に残った人だけを分析対象にすることで、本当は存在しない因果関係が「あるように見える」だけでなく、実在する関連を過大評価あるいは過小評価してしまうという、非常に厄介なバイアスです。

しかもその影響に気づかないまま推定を誤ることが多く、研究の信頼性を大きく損なうリスクがあります。

本記事では、選択バイアスの構造と見抜き方、DAGを用いた理解、IPWなどの対処法を、具体例とともにやさしく解説します。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• 選択バイアスとは何か ― “残った人”だけを分析すると推定がゆがむことを知る

• 選択バイアスの見抜き方 ― 間違った推定につながる“偏った選ばれ方”の特徴を知る

• 選択バイアスの対処法 ― 正しい推定を行うための考え方と基本的な手法を学ぶ

この記事は誰に向けて書かれているか

• 「選択バイアスって結局どういうこと？」と、論文を読んでも今ひとつピンとこない方

• 「Limitationsに“選択バイアスの可能性あり”と書いたけど…本当に理解できてるのかな」と不安なまま査読に出している方

• 選択バイアスをどう調整すればいいのか、方法論をきちんと押さえておきたい方

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

執筆者の紹介

氏名：MK
所属：研究所勤務
自己紹介：公衆衛生学修士、精神保健福祉士。大学卒業後、民間企業にて個人、企業、大学を対象としたメンタルヘルス支援に従事し、これまでに500を超える企業・官公庁・自治体で研修講師を務めた。働く人々の心の健康を支える現場に向き合う中で、支援の質と根拠のある実践の重要性を痛感し、公衆衛生大学院へ進学。科学的根拠に基づく精神保健支援の理論と方法に加え、疫学的研究手法を体系的に修得した。修了後は研究機関に所属し、精神保健分野における調査・研究活動に取り組んでいる。現場と学術をつなぐ実践知の蓄積を通じて、実効性のある支援と政策への貢献を目指している。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。

１．選択バイアスとは

選択バイアスとは、研究に残った人だけを分析対象にすることで因果関係が歪んでしまうことを指します。

選択バイアスは研究に参加する人としない人との違い、あるいは参加を継続する人と途中で研究からいなくなる人との違いから生じます。

すなわち、選択バイアスとは「データを分析するために、どんな人を選ぶか」で生じるバイアスです。少し難しく表現すると「原因と結果の共通効果（コライダー）で条件づける」ことで生じます。

「データを分析するために、どんな人を選ぶかって、どういうこと？」、「共通効果（コライダー）って何？」と疑問に思われていると思いますので、ここからは簡単な具体例を用いて、一つ一つ説明していきます。

ある研究者が「自分があくびをすると、他の人もあくびをするのだろうか？」ということを実験する研究を行いました。

研究者は自分があくびをして、周りの人がどう反応するかを観察しました。そして、実験の記録を確認してみると、確かに研究者があくびをすると、他の人もあくびをすることが多かったのです。

「自分が思った通り、あくびは他人に伝染するんだ！」と研究者は喜びましたが、実はこの研究には大きな問題が潜んでいました。

というのも、この研究では、実験の後に「あなたがあくびをしたという記録を、研究に使っても良いですか？」と確認し、同意を得られた人の結果だけを分析に使っていたのです。

その結果、次のような二つの問題が起こっていたのです。

1．恥ずかしがり屋の人は、もともとあくびを我慢する。
2．恥ずかしがり屋の人は、あくびを仕掛けられていたことを恥ずかしく感じ、参加を断ることが多かった。

つまり、研究への参加に同意した人たちは「研究者があくびをした時の記録：恥ずかしがり屋でない人、あくびをしやすい人たちが多く残った」「研究者があくびをしなかった時の記録：あくびをしやすい人も、そうでない人（恥ずかしがり屋の人）も含まれる」という偏りをもっていたのです。

この結果、「研究者があくびをする」→「周りの人もあくびをする」という関係が実際よりも強く見えてしまったのです。

つまり、「データを分析するために、どんな人を選ぶか」という過程そのものが、原因と結果には関係ないのに、まるで関係があるかのような「見せかけの関係」を作り出してしまうことがあります。これが選択バイアスです。

このように、選択バイアスは本当は存在しない因果関係があるように見えたり、関連を過大評価あるいは過小評価してしまい、研究の信頼性を大きく損なうリスクがあるのです。

２．選択バイアスの構造

ここからは、選択バイアスがどんな仕組みで起きるのか、もっと詳しく見ていきましょう （本稿ではDAGを用いながら選択バイアスの構造を読み解いていきますので、まずはDAGの基本の解説をお読みいただくことをお勧めします）。

DAGの徹底解説はこちら
DAGを徹底解説 | 基礎編：因果推論の必須ツールで、交絡因子を可視化する -
DAGを徹底解説 | 応用編：調整してはならない？コライダーと媒介変数の落とし穴 -

（なお、ここからの事例は話を簡単にするために、本来は「原因」と「結果」に関連が存在しないという前提で話をしていきます。）

最初の例は、妊婦さんが飲む「葉酸サプリ」と、生まれてくる赤ちゃんの「心臓の奇形」についての研究です（図１）。

「妊娠初期の葉酸サプリ摂取（A）」が、「赤ちゃんの心臓の奇形（Y）」のリスクを減らす効果があるのかどうかを知りたいとします。

赤ちゃんに「心臓の奇形（Y=1）」があると、「生まれる前の死亡リスク（C）」が高くなる（Y → C）。

一方で、「葉酸サプリ（A=1）」には心臓の奇形以外の異常を減らすことで、「生まれる前の死亡リスク（C）」を減らす効果があるとされている（A → C）。

図１をみると「葉酸サプリ（A）」と「心臓の奇形（Y）」の両方が、「生まれる前の死亡（C）」に影響を与えているのがわかるでしょうか。

そうです、「生まれる前の死亡（C）」は「葉酸サプリ（A）と心臓の奇形（Y）の共通効果（コライダー）」となっているのです。

もし、「無事に生まれた赤ちゃんだけ（C=0という条件で）」で分析する、つまり「葉酸サプリ（A）と心臓の奇形（Y）の共通効果（コライダー）」で条件づけるとどうなるでしょうか？

無事に生まれた（C=0）赤ちゃんの特徴

A=1（葉酸サプリを摂取）
・「葉酸サプリ」の効果で心臓の奇形以外の異常による死亡リスクが減少し、より多くの赤ちゃんが無事に生まれることが期待されます。
・「葉酸サプリ」が心臓の奇形以外の異常による死亡リスクを減らしたおかげで、心臓の奇形があっても（Y=1）無事に生まれてきた（C=0）、というケースも含まれる可能性があります。
・結果として「葉酸サプリあり（A=1）」のグループの中には「心臓の奇形あり（Y=1）」の赤ちゃんが見かけ上多くなるように見えてしまうかもしれません。

A=0（葉酸サプリを摂取しない）
・「葉酸サプリ」による心臓の奇形以外の死亡リスクの軽減がないため、もし「心臓の奇形（Y=1）」があれば「生まれる前の死亡あり（C=1）」のリスクがより顕著になります。
・結果として「心臓の奇形（Y=1）」の赤ちゃんは「生まれる前の死亡なし（C=0）」のグループからより多く「除外される」傾向にあります。
・したがって、葉酸サプリを摂取しない（A=0）のグループの中には、心臓の奇形あり（Y=1）の赤ちゃんが少ないように見えてしまうかもしれません。

このように「生まれる前の死亡なし（C=0）の赤ちゃんだけを対象にする」ことで、「葉酸サプリを摂取した方が、心臓の奇形の赤ちゃんが多い」という「見せかけの関連」が生まれてしまいます。これが、選択バイアスです。

もし、すべての赤ちゃん（生まれる前に亡くなってしまった赤ちゃんも含めて）を対象に研究ができていれば、「葉酸サプリ」と「心臓の奇形」の正しい関係がわかったかもしれません。

３．選択バイアスの具体例

ここから、医学研究において「選択バイアス」がどのように潜んでいるのか、具体例を見ていきます。

追跡不能による選択バイアス（differential loss to follow-up）

追跡から脱落のパターンが治療群と非治療群で異なる場合において、 研究から脱落しなかった人たちだけに絞って分析する際に生じるバイアスです。

例えば、HIVに感染した人たちへの「抗レトロウイルス治療（A）」が「３年後の死亡リスク（Y）」に影響するかを調べるとします（図２）。

「治療ありの人（A=1）」は、副作用が出る可能性があり、それが原因で研究から「脱落（C）」しやすい（A → C）。

「免疫抑制ありの人（U=1）」は「死亡リスク（Y＝1）」が高い（U → Y）。

「免疫抑制ありの人（U=1）」は、免疫抑制によって「重篤な症状（L）」が起こりやすく研究に参加し続けるのが難しいため「脱落（C）」しやすい（U → L → C）。

もし「脱落しなかった人たち（C=0という条件）」で分析するとどうなるでしょうか。

「治療ありの人（A=1）」は副作用によって「脱落する（C=1）」リスクがあるため、「脱落せずに残った人（C=0）」は比較的体力があり副作用が小さい人の割合が多くなるかもしれません。

また「免疫抑制あり（U=1）」の人も「重篤な症状（L=1）」により脱落しやすいため、同じく「脱落せずに残った人（C=0）」には「免疫抑制なしの人たち（U=0）」が多く残る可能性があります。

これにより、脱落せずに分析対象に含まれた治療群の人々が、もともと死亡リスクの低い人たちに偏る結果となります（治療による死亡リスクの改善を過大評価してしまうかもしれません）。

図２に沿って確認してみましょう。「治療（A）」と「免疫抑制（U）」の両方が「脱落（C）」に影響を与えているため、「脱落（C）」は「治療（A）と免疫抑制（U）の共通効果（コライダー）」となります。

すなわち、「脱落しなかった人たち（C=0）」という対象者の選び方は、「治療（A）と免疫抑制（U）の共通効果（コライダー）」で条件づけることとなり、「治療（A）」と「死亡リスク（Y）」の関係に見せかけの関連が生まれ、つまり選択バイアスが生じるのです。

先ほど選択バイアスは「原因と結果の共通結果（コライダー）」で条件づけることで生じると説明しましたが、より厳密には以下のように説明することができます。

選択バイアスは「二つの変数」の共通効果（コライダー）を条件とすることから生じる

「二つの変数」とは、
①「原因」または「その影響を受ける変数」
②「結果」または「その影響を受ける変数」（ここでは死亡リスク（Y）と免疫抑制（U））

欠測データバイアス、非回答バイアス

個人が情報を提供することに消極的であったり、研究訪問を逃したなどの理由でデータの欠測が生じる場合があります。また、調査に回答しなかった人たちが、答えた人たちとは健康状態や生活習慣などが大きく異なるような場合、つまり「無回答者が回答者とが系統的に異なる」場合に、完全なデータを持つ個人のみに解析を制限するとバイアスが生じる可能性があります。

冒頭の具体例で挙げた「あくびを観察する研究」で、「あくびをしたことが恥ずかしく、研究への参加を断った例」がこれにあたります。

健康労働者バイアス

健康で身体が丈夫な人ほど労働を続けることができるため、その職場で働いている人たちを分析対象とすると、結果が健康な人たちのデータに偏ることによるバイアス です。

例えば「ある化学物質（A）」にさらされることが、工場で働く人たちの「死亡リスク（Y）」に影響を与えるかを知りたいとします（図３）。

「健康な人（U）」ほど「死亡リスク（Y）」が低く（U → Y）、職場の健康診断でも「異常所見（L）」がなく「仕事を続ける（C=0）」ことができる（U → L → C）。

化学物質にさらされると、喘息になってしまうなどの理由で仕事を続けられなくなることがある（A → C）。

もし「仕事をしている人たち（C=0という条件で）」で分析するとどうなるでしょうか。

「化学物質にさらされている（A=1）」のに「仕事を続けられている人（C=0）」は、もともと身体が丈夫で「健康な人（U=1）」が多かったかもしれません（あまり健康ではない人は、化学物質の暴露に耐えられず労働から脱落しているかもしれません）。

逆に「化学物質にさらされていない人（A=0）」で「仕事を続けられている人（C=0）」の中には、もともと「あまり健康ではない（U=0）けれど、化学物質の影響がないから仕事を続けられている」人もいるかもしれません。

「仕事を続けている人たち（C=0）」の特徴

化学物質にさらされている人たち（A=1）
・「健康な人たち（U=1）」が多く在籍している（あまり健康でない人たちは、化学物質への暴露により労働から脱落している）。

化学物質にさらされていない人（A=0）
・「健康な人たち（U=1）」だけでなく「あまり健康でない人（U=0）」も多く含まれている。

つまり「仕事をしている人たち（C=0）」を対象とした場合、「化学物質にさらされた人たち（A=1）」の方がもともと健康で死亡リスクが低い人たち（U → Y）の割合が多く、死亡リスクが低く算出される可能性があります。

その結果、まるで「化学物質が死亡リスクを減らしている」かのような見せかけの関係が生まれてしまいます。これが健康労働者バイアスの成り立ちです。

自己選択バイアス（Self-selection）

これは「研究に参加するかどうか」を自分で決める場合に起こりやすいバイアスです。

例えば、とある研究で「喫煙（A）」が「冠状動脈疾患（Y）」に影響を与えるかを調べたい知りたいとします（図４-１）。

「家族に心臓病の人がいる（U=1）」場合、心臓病になりやすく（U → Y）、「心疾患への意識が高まり（L=1）」、研究に参加する（U → L → C）かもしれません。

「健康的なライフスタイルを送っている人（W）」は、喫煙しない傾向がある（W → A）し、研究にも積極的に参加する（W → C）かもしれません。

つまり「健康的なライフスタイル（W）」と「家族歴（U）」の両方が「研究参加（C）」に影響を与えており、「研究への参加（C）」は「健康的なライフスタイル（W）と家族歴（U）の共通効果（コライダー）」となっています。（図４-２）

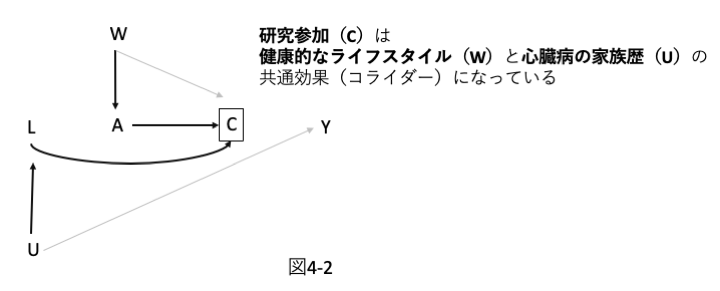
もし「参加に同意した人たち（C=0という条件で）」で分析するとどうなるでしょうか。

参加に同意した人たち（C=0）の特徴

喫煙者（A=1）
もしかしたら「心臓病の家族歴（U）」がある人たちだったかもしれません。
なぜなら、家族歴がある人は、心臓病のリスクへの意識が高い（L=1）ために研究に参加した可能性があるからです。

非喫煙者（A=0）
もともと「健康的なライフスタイル（W=1）」を送っている人が多く、健康意識が高いため研究にも参加している、という可能性があります。

「喫煙者（A=1）」には「心臓病の家族歴がある人（U=1）」がより多く含まれる
「非喫煙者（A=0）」には「健康的なライフスタイルの人（W=1）」がより多く含まれる

つまり、「参加に同意した人たち（C=0）」において、「喫煙者（A=1）」には「心臓病の家族歴がある人（U=1）」がより多く含まれるため、「冠動脈疾患に罹患（Y=1）」する人が多く（U → Y）、「非喫煙者（A=0）」には「健康的なライフスタイルの人（W=1）」がより多く含まれるため「冠動脈疾患に罹患しない（Y=0）」人が多く含まれるかもしれません。

その結果、「喫煙者は冠動脈疾患を罹患しやすい」という見かけ上の関連を生み、選択バイアスが生じる可能性があるのです。

治療や暴露が選択に影響することで生じる選択バイアス （Selection affected by treatment received before study entry）

これは、研究が始まるよりも前に、すでに暴露（治療）を受けている場合に起こりやすいバイアスです。

例えば、50歳の人を対象として、生涯にわたる喫煙歴が、研究開始後10年間の心血管疾患への影響をみるとしましょう。

１日に１箱タバコを吸うような重度の喫煙者がいることを想像してみてください。

そういった方ほど早くに亡くなってしまい、50歳になる前に亡くなってしまう方も数多くいるわけです。

つまり、この研究デザインにおいては「50歳になる前に亡くなるような重度喫煙者は、そもそも研究に参加できない」という状況にあります。

したがって、この研究に参加している喫煙者は「50歳より長生きすることができる、比較的健康な喫煙者」に限定される選択バイアスによって、喫煙と心血管疾患の本来の因果関係が歪んでしまう可能性があります。

４．交絡と選択バイアスの違い

ここまで、選択バイアスは「原因と結果の共通効果（コライダー）」を条件づけることによって生じることを説明してきました。

一方で、因果効果の推定を歪ませる代表的な要因として「交絡」があります。交絡は「原因と結果の共通原因」であり、交絡によって生じるバイアスを交絡バイアスと呼ぶのでした。

交絡についての詳細な解説はこちら
交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

選択バイアスと交絡はどちらも推定をゆがめる要因ですが、この違いを理解するのはとても大切です。なぜなら「原因と結果の間の本当の関係を、何が邪魔しているのか」を理解することで、推定のゆがみを防ぐ対応ができるからです。

例えば、消防士の人たちを対象に「身体的に活動的であること（A）」が「心臓病のリスク（Y）」に影響するかを調べるとします（図５）。

この研究は「消防士に限定されている（C=0）」ことがポイントです。

「両親の社会経済的地位（L）」が、その人が消防士になるかどうかに影響を与えるし（L → C）、また子どもの頃の食生活などを通じて心臓病のリスクにも影響を与える（L → Y）と考えることができます。

「運動への興味（U）」という変数は、消防士になるかどうかに影響を与えるし（U → C）、「身体的に活動的であるかどうか（A）」にも影響を与えます（U → A）。

しかし、消防士の人たち（C=0という条件で）で分析するとどうなるでしょうか。

U（Aに影響を与える）とL（Yに影響を与える）の共通結果（コライダー）に条件づけることになり、「身体的に活動的であること（A）」と「心臓病のリスク（Y）」に見せかけの関連が生まれる選択バイアスが生じます。

そのため「消防士の人たち（C=0）」に限定する場合は、「両親の社会経済的地位（L）」で条件づけることで「身体的に活動的であること（A）」と「心臓病のリスク（Y）」の経路を遮断してバイアスを防ぐことができます。

一方で消防士の人たちに限定されない場合は、この因果構造では、「両親の社会経済的地位（L）」は「身体的に活動的であること（A）」と「心臓病のリスク（Y）」の「共通の原因」にならないため、交絡ではありません。そのため、「身体的に活動的であること（A）」と「心臓病のリスク（Y）」の経路は遮断されたままなので、「両親の社会経済的地位（L）」を条件づけることは必要ではありません。

このように、原因と結果の間の本当の関係を邪魔しているのが「選択バイアス」なのか「交絡」なのかをDAGを用いて検討することで、研究者間の意思疎通を促進して、調整すべき・すべきでない変数を明らかにすることができるのです。

RCTと交絡・選択バイアス

ここまで医学研究に潜む様々な選択バイアスのパターンを見てきました。

実は、因果効果を推定するゴールドスタンダードであるランダム化比較試験（RCT）でも、選択バイアスは注意が必要になります。

「原因（A）」と「結果（Y）」に共通原因である交絡がない場合は、「A=1」と「A=0」で背景因子がそろっており、RCTと同じ条件を満たすことになるため因果推定が可能になります。すなわち、RCTは交絡を防ぎます。

RCTと交絡の関係についてはこちらの記事で解説しています
Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）により実現する因果推論の必須条件 -

一方、選択バイアスはどうでしょうか。ある薬（治療A）の症状（結果Y）に対する効果を調べるRCTを考えてみましょう。

薬の副作用によって脱落が発生する場合、治療A=1にはより健康な人が残る可能性が高いかもしれません。

その場合、ランダム化でせっかくそろっていたA=1とA=0の間の背景因子のバランスが崩れます。そのため、治療A と結果Yの因果推定にゆがみが生じてしまいます。

すなわち、RCTは交絡を防ぎますが、ランダム化の後に解析の対象になる人が選ばれることによってバイアスが生じ得ます。そのため、RCTでも選択バイアスからは逃れることができないのです。

５．打ち切り（censoring）と選択バイアス

打ち切り（censoring）がある場合の選択バイアスについて考えてみます。

打ち切り（censoring）とは、イベントが発生する前に観察が終了した、すなわち特定の時点まではイベントが発生していないことが分かっているが、その後のイベント発生が確認できない場合を指します。

ところで先ほど追跡不能（Loss to follow-up）という単語が出てきました。これと打ち切り（censoring）は何が違うのでしょうか。

追跡不能（Loss to follow-up）は、何らかの理由で連絡が途絶え、イベントの発生の有無がわからない場合を指します。

先ほど説明した通り、追跡不能（Loss to follow-up）は追跡できなかった理由が原因や結果と関連している可能性があり、追跡できた人だけで解析することは原因と結果の共通効果（コライダー）での条件付けとなり選択バイアスが生じ得ます。

一方、打ち切り（censoring）は「結果に影響を与えてなければ」無視してもよいとされます。しかし、打ち切り（censoring）が「原因と結果に影響を与えている場合」は選択バイアスが生じ得ます。

例えば、 HIV の「治療効果（Y）」 を観察する研究で、「打ち切りで脱落した人（C=1）」の一部が、「その後の治療を受けられなかったために予後が悪化した」と考えられる場合、「脱落 C」は「アウトカムY」に影響を与えているため、因果効果の推定時に「脱落C」 に関する交絡の調整が必要になります。

すなわち、打ち切り（censoring）の場合は「脱落がなかった場合に何が起こったか」を因果推定に反映する必要があります。

つまり、「全員が治療を受け、かつ脱落しなかった場合のリスク」と「全員が治療を受けず、かつ脱落しなかった場合のリスク」の比較する必要があるのです

言い換えれば、打ち切り（censoring）の情報を無視せず、その情報も考慮に入れて分析を進める、ということです。

具体的には、「打ち切り自体をもう一つの『治療』と見なして、その影響も同時に調整する」という考え方を導入するということです。これによって、打ち切りによって生じる選択バイアスを適切に補正し、より正確な因果効果を推定することが可能になります。

６．選択＝常にバイアスではない

ここまで、選択バイアスが起こる様々なケースを見てきましたが、共通効果（コライダー）を条件づけても選択バイアスが起こらないパターンもあります。

「手術（A）」とある「遺伝子（E）」が「死亡（Y）」に関連する場合、「死亡（Y）」は「手術（A）と遺伝子（E）の共通効果（コライダー）」のため、「死亡（Y）」で条件づけると手術（A）と遺伝子（E）に見せかけの関連が生じます（図６）。

これに条件を足して、手術（A）が腫瘍の切除を通じて生存に影響する一方、遺伝子（E）は低密度リポタンパク質コレステロール（LDL-C）値を上昇させることで心臓発作のリスクを高め、その結果として生存に影響する状況を考えてみます（図７）。

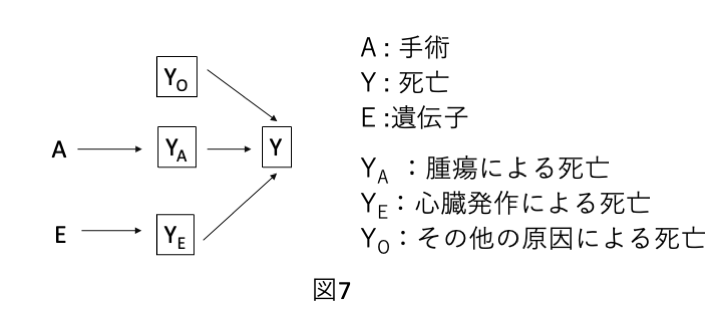
このシナリオでは、三つの原因別死亡アウトカムを考えることができます。

１．腫瘍による死亡（Y A ）
２．心臓発作による死亡（Y E ）
３．その他の原因による死亡（Y O ）

観察される死亡（Y）は、Y A 、Y E 、またはY O のいずれかが「死亡」である場合にY=1となり、 すべてが０（非死亡）である場合にY=0となります。

この場合、死亡（Y）は「手術（A）と遺伝子（E）の共通効果（コライダー）である生存（Y=0）」に条件づけることは、Y A 、Y E 、Y O のすべててが０であることを意味する、すなわち、Y A =0、Y E=0 、Y O=0 で条件づけられてブロックされるため、手術（A）と遺伝子（E）に見せかけの関連は生じません。

７．選択バイアスをどう調整するか

ここまで、選択バイアスがいかに因果推論の結果を歪めてしまう可能性があるか、また、多くの場合、選択バイアスを避けることは困難であることがご理解いただけたかと思います。

しかし、データ分析の段階で、統計モデルを用いて選択バイアスを補正することもできます。

一例として、逆確率重み付け（Inverse Probability Weighting：IPW）いう方法があります。これは「研究に残った人たち（C=0）」に、特別な「重み」をつけることで、まるで「参加から脱落した人たち（C=1）」の影響を考慮するように分析する方法です。

IPWの徹底解説はこちら
逆確率重み付け（Inverse Probability Weighting）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

具体的には、脱落した人たちと似たような特徴を持っているのに、研究に残った人たちに少し大きめの重みを付けて脱落したことによって生じたデータの偏りを補正します。

これにより、脱落した人たちも含めた「もし全員が参加していたら」という状況に近づけて、より正確な因果関係を推定に近づきます。

ただし、そのためには選択バイアスをなるべく避けたり、あとで補正できるように、研究計画の段階でフォローアップがなるべく起きないようにする工夫や、IPWに必要な情報、どういう人が残りどういう人が脱落したのか、選択のメカニズムに関連するデータの測定を組み込んでおくことが不可欠です。

８．まとめ

• 選択バイアスは「研究に残った人」と「残らなかった人」の違いによって生じ、研究に残った人だけを解析対象にすると推定結果が歪む可能性がある。

• 選択バイアスは「原因と結果の共通効果（コライダー）」で条件づけることで生じる。

• 選択バイアスへの対処法としてIPWといった統計手法で調整が可能だが、研究計画の段階で選択バイアスが生じにくい設計と、生じた際の補正手段をあらかじめ組み込んでおくことが重要。

参考文献

• 井上浩輔．医学研究のための因果推論レクチャー．医学書院 2024

• 小松裕和, 鈴木越治, 土居弘幸. "臨床医のための疫学シリーズ: 地域中核病院で行う臨床研究 第 4 回 バイアスの考え方, 結果の解釈の仕方 (疫学各論 3)." 日本救急医学会雑誌 20.9 (2009): 794-800. https://doi.org/10.3893/jjaam.20.794

• KENNETH J.ROTHMAN [著]ほか. ロスマンの疫学 : 科学的思考への誘い. 第2版, 篠原出版新社 2013

• UNBOUNDEDLY. 選択（セレクション）バイアスとは？人によって定義が違うので整理してみた。選択（セレクション）バイアスとは？人によって定義が違うので整理してみた。 - Unboundedly

• mMEDICI Channel.【耳から学ぶ因果推論】選択バイアス、消えた患者が結果を歪める？【疫学専門家監修】【耳から学ぶ因果推論】選択バイアス、消えた患者が結果を歪める？【疫学専門家監修】

• mMEDICI Library.【疫学専門家監修】DAGを徹底解説 | 基礎編：因果推論の必須ツールで、交絡因子を可視化する - ゼロから学ぶ因果推論 vol.12-1 https://mmedici.co.jp/mmedici-library/XVa3o2SH

• mMEDICI Library. 【疫学専門家監修】交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 - ゼロから学ぶ因果推論 vol.13 【疫学専門家監修】交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 - ゼロから学ぶ因果推論 vol.13 ｜mMEDICI Library

参考図書：『Causal Inference: What If』

Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。

mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。

そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。

mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る｜ 無料体験に申し込む

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する

  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？-