
【疫学専門家監修】標準化(Standardization)を徹底解説 - 交絡調整の基本をわかりやすく図解 - vol.5
2025.01.06
シリーズ紹介|ゼロから学ぶ因果推論
「医学研究は難しい」、きっと多くの方がそう感じているでしょう。
因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。
因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。
「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。
はじめに
因果推論について学ぶ中で登場する「標準化:Standardization」。
初めて目にした時に「難しそう…」とつまずいてしまった方も多いのではないでしょうか?
この記事では初めて学ぶ方や数式が苦手な方でも確実に理解を深められる様に、可能な限り平易な言葉で、図やイラストを用いながら標準化について解説していきます。
mMEDICI Library | ひらけ、叡智の扉
叡智の扉を、全ての人が開けるように——。
学びは、限られた豊かな人々だけの特権ではありません。
経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。
mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。
隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。
「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。
この記事のまとめ
この記事を読むと分かること
どうして標準化が必要なのか理解できる
簡単なデータに対して、標準化を実践できる
数式が表している意味を言語化できる
この記事は誰に向けて書いているか
因果推論について初めて学ぶ方
統計学や数式が苦手な方
標準化について理解を深めたい方
因果推論シリーズ
vol.1:因果推論の出発点 - 因果と関連の違いとは? -
vol.2:因果効果の基本を徹底解説 - Individual Causal Effect(個人因果効果)とAverage Causal Effect(平均因果効果)の違いとは? -
vol.3:初心者のためのTarget Trial Emulation(TTE)
- Part 1 ; ETAFOCAフレームワークについて
- Part 2 ; 三つの時点で考えるバイアスとその対処法
- Part 3 ; 論文の実例で理解を深めるTTEvol.4:Exchangeability(交換可能性)を徹底解説 - Randomization(ランダム化)が実現する因果推論の必須条件 -
vol.5:Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.6:Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.7:Consistency(一致性)を徹底解説 - 観測データと反事実アウトカムを一致させよ -
vol.8:Positivity(正値性)を徹底解説 - 因果推論の落とし穴を回避せよ -
vol.9:Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
vol.10:効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか? -
vol.11:交互作用を徹底解説 - 複数の介入による相乗効果 -
vol.12:DAGを徹底解説
vol.13:交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
vol.14:選択バイアスを徹底解説 - 消えた患者が結果を歪める?-
執筆者の紹介
氏名:岡部陽介
所属:理学療法士養成校 専任教員
経歴:理学療法士として5年間の臨床経験を経て、現在は理学療法士養成校で教員として勤務。ヘルスコミュニケーション、医療者と患者の共有意思決定(SDM:Shared Decision making)に関心を持つ。
編集者
氏名:菊池祐介
所属:mMEDICI株式会社
専門性:作業療法学修士。首都大学東京(現東京都立大学)・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。
監修者
氏名:廣瀬直紀
所属:mMEDICI株式会社
専門性:保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。
はじめに
因果推論を学ぶ途中で「標準化(Standardization)」という言葉が登場し、何やら難しい数式が現れて「こんなのわからないよ…」と挫折してしまった方も多いのではないでしょうか?
私も初めて標準化について触れた時、いきなり難しそうな数式を目してポッキリと心が折れてしまったことを覚えています。
こんなやつです。
Σl E[Y|L = l, A = a] × Pr [L = l]そもそも私は高校時代の数学もろくにできなかったですし、ややこしい数式を見るだけで気分が悪くなってしまうのですが、「なんとかして因果推論を学ぶんだ!」という熱い気持ちで標準化の数式に挑んでいったわけです。
もちろん、結果は言わずもがな。
「”Σ”ってなんだっけ?」「そうか、”シグマ”って読むんだったな!」というところから始まり、「で、結局なんなの?」「Σの横にあるもやしみたいな記号は何??」とあっけなく壁にぶち当たったわけです。
こうして早くも2度目の挫折を味わい、参考書で標準化という文字を目にするだけで動悸を感じた時期もありました。
さて、このように「標準化で挫折の経験者」の私ですが、幸運なことに専門家から因果推論を学ぶ機会を手にし、こうして皆さんに標準化の解説記事を提供させていただいております。
mJOHNSNOWの「Causal Inference What If」の輪読会では標準化のパートを担当し、恥ずかしながら皆様に講義させて頂きました。
数学が大の苦手で、因果推論を0から学んできた筆者だからこそ、標準化の理解を進めるために大切な文脈や、初学者つまづきやすいポイントを踏まえた説明ができると思っています。
標準化について理解を深めることは、これまで学んできた因果推論の考え方に基づき「いざ、因果推論を実践する」ための土台を作ることでもあります。
そのため、いきなり「標準化」の理論や数式に触れるのではなく、因果推論においてなぜ標準化という手法が必要なのか、これまでのmMEDICI Libraryで学んできた因果推論の理論や考え方を一つひとつ整理しながら標準化の理解に結びつけていきます。
この記事を最後まで読み終えた時にはきっと、
どうして標準化が必要なのか理解できる
簡単なデータに対して、標準化を実践できる
数式が表している意味を言語化できる
ようになっていることでしょう。
それでは、次の章から最初の一歩を進めていきましょう。
どうして標準化が必要なのか
「そもそもどうして標準化が必要なの?」「標準化って結局なにをしているの?」を考えていくと、意外にシンプルです。
標準化を簡単に言い表すと「交絡因子に対処してExchangeabilityを成立させて、因果推論を実現するための工夫」のひとつです。
「全然簡単じゃない!」と思った方。ご安心ください。
まずは下の図をご覧ください。

因果推論で目指しているのは
現実で得ることができる結果:
「治療ありの人たち」 と 「治療なしの人たち」の結果の差から、
現実では得られない結果:
「もし全員が治療あり」の場合と「もし全員が治療なし」の場合の結果の差
を推論することでしたね。
また、前回の記事では、RandomizationによってExchangeabilityが期待されるため、現実で得られたデータから因果効果を推論できるということを学びました。
<Randomization とExchangeabilityについて>
図で表すとこんな感じです。
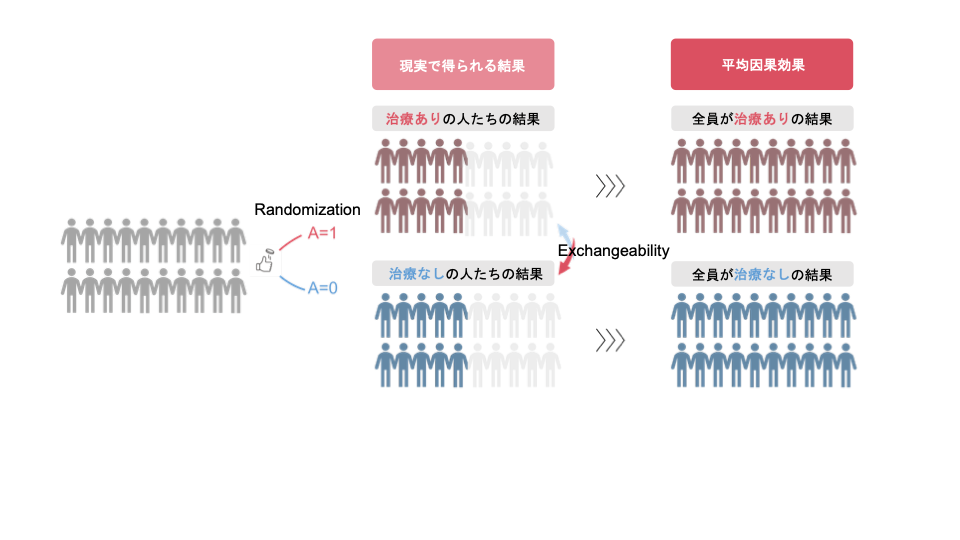
ただし、以下のようにRandomizationによってExchangeabilityが成立しないケースもあります。
交絡因子が偏ってしまう
サンプルサイズが小さい
途中で治療を離脱してしまう
そんなときに登場するのが、標準化という手法です。
以下のようなイメージです。
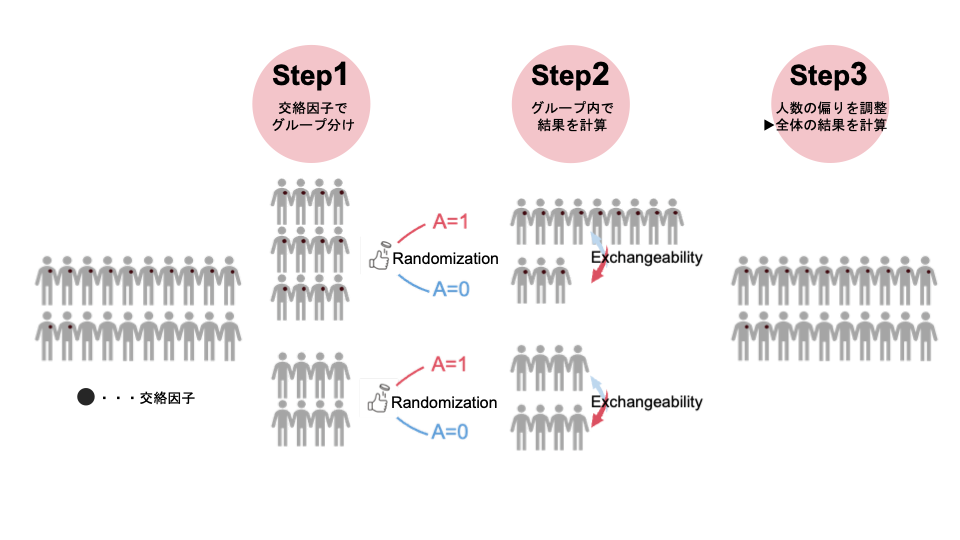
大まかな説明ですが、
Step1:交絡因子ごとにグループ分け
Step2:グループ内でRandomizationして治療を割り付け
Step3:最後に人数の偏りを調整するという流れです。
Step1で「治療の割り付け後に交絡因子が偏って困るのなら、割り付ける前に分けてしまおう!」というわけです。
「全員が交絡因子あり」「全員が交絡因子なし」のグループを作ってあげれば、グループの中では交絡因子の有無が偏ることはなくなりますね。
あとは、Step2のようにグループ内でランダムに治療を割り付けることで、交絡因子あり・なしのグループ内でのExchangeabilityが成り立つのです。
この章の冒頭で出てきた「標準化は、交絡因子を調整してExchangeabilityを成立させて、因果推論を実現するための工夫」という表現ですが、なんとなくイメージができたでしょうか?
難しい数式もなく、やってることはいたってシンプルですよね。
とりあえずは、ここまでを理解できれば標準化の最初のゴールはひとまずクリアしたと思ってよいと思います。
次の章から少しずつ数式も登場してきますが、わからなくなったらこの図を見返していただき、「とりあえず、交絡因子をよしなに調整して、Exchengeability を成立させているんや」と割り切るのが吉です。
標準化で何を成し遂げたいのか見失わない様に、いったりきたりしながら読み進めていただけたらと思います。
話は少しそれますが、因果推論の参考書や論文を読んでいると様々な分析手法が登場しますが、やはり根底には「交絡因子を調整してExchangeabilityを成立させる」という目的があったりします。
逆に言えば、複雑で高度な分析手法が必要とされる背景には、研究において交絡因子の問題は極めて難しく、ある手法や研究デザインで一筋縄に解消できるものではないという事が推し量れますね。
最初から難解な分析手法を理解するのは大変ですので、とにかく「因果推論の世界では、何とかしてExchangeabilityを整えるために、あれこれと工夫するのだ」と念頭において前に進んでいきましょう。
ここまでのまとめ
・RandomizationでExchangeabilityが成り立たない事もある
・そんなとき、標準化によって交絡因子を調整できる
・標準化によりExchangeabilityがより成立し、より頑健な因果推論が可能になる 少し踏み込んだ理解を
さて、標準化で何をやっているのかをイメージできたところで、ここからは、これまでmMEDICI Libraryで学んできた因果推論の知識を使いながら理解を深めていきましょう。
まずは、因果推論で知りたいことを復習していきましょう。
例えば、発熱患者に対する治療A(解熱剤)による結果(重症化リスク)を検証したいとき、治療Aの平均因果効果は以下の式で表す事ができます。

この時に問題となるのが、潜在的な結果である
E[Y^{a=1}=1]と E[Y^{a=0}=1]
の双方を同時に観測することは不可能であることです。
例えば20人の患者さんがいて「20人全員が治療を受けた」場合には、「もしも、20人全員が治療を受けていなかったら…」の未来を誰も知ることはできないのです。
(いわゆる因果推論の根本問題)
因果推論ではこの問題に対してConsistency やExchangeabilityといった仮定をおきながら、現実の世界において観測できるデータから因果効果を求めていくことになります。
<RandomizationとExchangeabilityについて>
復習も兼ねて、
現実の結果:E[Y=1|A=1]―E[Y=1|A=0]から
平均因果効果:E[Y^{a=1}=1]と E[Y^{a=0}=1]を導いていきましょう。
まず、Consistencyより以下のように変換することができます。

この式を言葉で補足してみると

Cosistencyによって現実の結果から潜在的な結果に変換することができましたね。
しかしまだ、「治療ありの人たち」と「治療なしの人たち」というくくりがあり、因果推論で目指している「全員が治療ありなら」「全員が治療なしなら」を表すことができていませんね。
(言い換えると「治療Aあり人たち」という条件で限定されていて、ややこしい表現をすると治療Aで条件づけられた重症化リスクとなります。いわゆる条件付き期待値というやつです。)
さて、次のステップです。
治療Aがランダムに割り付けられている場合には、Exchangeabilityが成り立ち、数式では以下のように表すことできます。

今までの説明を一連の式で表すと

このようにして、
現実の結果 E[Y|A=1]- E[Y|A=0]から
平均因果効果 E[Y^{a=1}=1]- E[Y^{a=0}=1]を導くことができました。
なぜ標準化?
さて、これだけを見ると「ランダム化試験を行えば因果推論が実現できる!」と思えますし、この記事の主役である「標準化」の出番はないように思えます。
しかしながら、前の章でも少し触れた様に「ランダム化によりExchangeabilityを成立させることが難しい場合」があります。
例えば、ランダム化試験を計画して治療を無作為に割り付けたとしても、小規模なサンプルであれば交絡因子が治療群と非治療群とで偏ってしまう可能性が生じてしまいます。
また、治療を割り付けた時点で交絡因子の偏りがなかったとしても、対象者が途中で離脱してしまう、割り付けられた通りに治療を継続できないなど、様々な理由によりExchangeabilityが崩れてしまう可能性があります。
このような理由から、ランダム化試験においてもExchangeabilityが成り立たない可能性があると考えるのが自然かもしれません。
そもそもランダム化試験を実施すること自体がとても大変なことでもあります。
あらゆる交絡因子を均等にし、完全なExchangeability が成立するような「理想的なランダム化試験」を行うためには、極めて大規模なデータ、時間、労力、費用を費やす必要があり、これを実現することは至難を極めるといえるでしょう。
(この記事ではランダム化試験を想定して話を進めていきますが、そもそもリアルワールドデータを扱うような観察研究おいてはランダム化そのものが難しい場合があります。例えば喫煙の有無による呼吸器疾患の発生率を調べたいというような場合、「喫煙」「非喫煙」をランダムに割り付ける、ということは倫理的に非現実的ですよね。)
この様に、現実的には「ランダム化により交絡因子の影響をなくし、Exchangeabilityを成立させること」はとても難しいのです。
そんなことを言ってしまっては「そもそも、因果推論なんてできっこないのでは?」と途方に暮れてしまうかもしれません。
ここでようやく、標準化の出番がやってくるのです。
次の章では、ランダム化によって解決できないExchangeabilityの問題を、標準化によって解決していきます。
標準化(Standardization)の準備をしよう〜層別化〜
標準化の理論を理解していくために、以下のような対象集団を想定して説明を進めていきます。

発熱患者20名に対する治療A(解熱剤)による重症化リスクを検証していきます。
全体の20名のうち12名は、発熱の重症化を高めうる基礎疾患(例えば呼吸器疾患など)、いわゆる交絡因子を有しています。
ここでは20名しかいませんので、治療Aを20名をランダムに割り付けたとしても交絡因子が治療あり・治療なしで均等になる確率はかなり低くなり(この場合は約35%になります)、交絡因子が治療あり・治療なしの群間で偏る可能性があります。
交絡因子の偏りを解消するためのシンプルな方法が、ランダム化を行う前に集団を交絡因子Lがある人たち(L=1)とない人たち(L=0)に分ける方法です。
これを層別化といいます。
層別化した上で、それぞれの層(L=1とL=0)の中で治療Aをランダムに割り付けます。
ここでは、
L=1のグループにおいては、75%の確率で治療Aを割り付け、
L=0のグループにおいては、50%の確率で治療Aを割り付けています。

この時、L=1とL=0のそれぞれの層の中においてRandomizationが行われているため、それぞれの層の中においてExchangeability が成立することになります。
このように、
ある条件のものでRandomizationが成り立つことをConditional Randomizationと呼び、
ある条件のものでExchangeabilityが成り立つことをConditional Exchangeabilityと呼びます。
Conditional Exchangeabilityが成り立つことで、以下のように表すことができます。

一番上の式に注目すると、
L=1の人たちの中で、治療Aありの人たちの重症化リスクは、
L=1の人たち全員が治療Aを受けた場合の重症化リスクと等しいということができます。

層別化された結果がもつ意味
このとき注意したいのは、層別化で得られた結果が表しているのはあくまでも
「L=0の人たち」「L=1の人たち」それぞれの結果にすぎない、ということです。
ここでいま一度、私たちが因果推論で知りたいことを再確認しましょう。
平均因果効果 E[Y^{a=1}=1]- E[Y^{a=0}=0]
そうです、「全員が治療ありの場合・全員が治療なしの場合」の結果の差分を知りたいのでしたね。
だったら、単純にL=0の人たちとL=1の人たちの結果を足して2で割ってあげれば、「L=0、1も合わせた全体の平均」がわかり、「全員が治療あり・全員が治療なしの結果」を求められるのでは、と思えるかもしれません。

残念ながら、それでは少し問題が生じてしまいます。
例えば、この集団では全体の人数20名に対して
L=1が12名(60%)
L=0が8名(40%)を占め、人数の偏りが生じています。
両群の結果をそのまま平均してしまうと、
「全体の集団の6割を占める人たちの結果」と「全体の集団の4割しかない人たちの結果」を等しく扱ってしまいます。
つまり「全員が治療Aを受けた結果」を知りたいにも関わらず、
「全体の集団の6割を占める人たちの結果」を、相対的に軽くしてしまうことになります。
そこで標準化では、
「L=1、L=0の人数」が「全体の人数に占める割合」に注目して交絡因子を調整し、
「L=1もL=0も含めた全体における結果」を導いて行きます。
標準化の計算をしてみよう
方法は非常にシンプルで、
層別に求めた結果に、それぞれのグループの人数の割合をかける。
ただそれだけです。
「L=1の人たちの結果に60%の重み」
「L=0の人たちの結果は40%の重み」を与えてあげる事で、
人数の偏りによる結果の歪みを整えてあげるというイメージです。
まずは、L=1、L=0それぞれにおいて、A=1(治療あり)とA=0(治療なし)における重症化リスクを計算していきます。
イラストを見ながら数えてみると簡単ですね。

これを、数式と並べてみましょう。

次に、それぞれの結果に、それぞれの人数の割合を掛け合わせます。

それぞれの人数の割合で重み付けしたことになるので、
L=1とL=0の結果をそのまま足し合わせることで、
L=1の人もL=0の人も含めた全員の重症化リスクの平均を計算することができます。(これを重み付け平均といいます)
まずは治療Aありを計算(=全員が治療ありの重症化リスク)

治療ありの場合の重症化リスクは50%であることがわかります。
続いて治療なしを計算(=全員が治療なしの重症化リスク)

治療なしの場合の重症化リスクは50%であることがわかります。
これで、私たちが知りたかった
E[Y^{a=1}=1] と E[Y^{a=0}=0]
すなわち「全員が治療Aを受けた場合」と「全員が治療Aを受けなかった場合」の結果を導くことができました。
あとは、この値を使って平均因果効果を求めてみましょう。
E[Y^{a=1}=1] - E[Y^{a=0}=0]=0.5-0.5=0つまり今回の例では、発熱者に対する治療A(風邪薬)は、治療あり・なしともに重症化リスクが50%で等しいため、
「治療Aは重量化リスクに影響しない」ということができそうです。
標準化のステップ
1.交絡因子で層別化
2.各層の中でランダム割り付け
3.各層の中で結果を計算
4.全体に占める人数の割合をかける
5.各層の結果を足し合わせる標準化しなかったらどうなるの?
さて、前のセクションでは標準化によってひとつ結論を導くことができました。
では、実際に標準化をした場合としなかった場合とでどのような違いが生じるのでしょうか。
層別化のみ行い、標準化による重み付けをしなかった場合をシミュレーションしてみましょう。
L=1とL=0の結果を単純に平均しています。
(標準化の式と比べやすいように、それぞれに0.5をかけるという表記にしています)


治療あり・なしそれぞれの重症化リスクは
L=1 :2/3 = 33%、L=0:1/4 = 25%となっており、
L=1の人たちの方がより重症化リスクが高い傾向にあることがわかります。
標準化しなかった場合の結果は、
治療ありの重症化リスク=45%
治療なしの重症化リスク=45%となり、
標準化した場合の結果
治療ありの重症化リスク=50%
治療なしの重症化リスク=50%
と比べて、それぞれ重症化リスクを5%低く計算していることがわかります。
つまり、「全員の集団の6割を占めている、基礎疾患ありの人たちの、より高い重症化リスク(33%)」の影響を小さくし、
「基礎疾患がない(L=0)人たちの、より低い重症化リスク(1/4 = 25%)」の影響を大きくした結果ということができ、交絡因子の有無によって歪められた結果ともいえます。
標準化することで、集団全体における交絡因子の影響を調整することができ、より正確にデータを読み解くことができることが分かります。
標準化の限界
ここまで、交絡因子Lがひとつだけの状況を想定して考えてきました。
しかし、現実の世界では「交絡因子がひとつだけ」という状況は稀で、実際には複数の交絡因子を調整しなければなりません。
例えば交絡因子が1つの場合は、
[治療あり・なし] × [交絡因子あり・なし]
2 × 2=4層 にわかれました。

これが、交絡因子が2つの場合には、
[交絡因子①あり・なし]×[交絡因子②あり・なし]×[治療あり・なし]
2×2×2=8層にわかれることになります。

このように、調整すべき因子が増えるごとに層の数が増えていくことになります。
あり・なしの2水準で表せる交絡因子が10個ある場合には、治療Aの割り付けも掛け合わせると2,048個の層ができることになります。
この場合、たとえ10,000人のデータがあって全ての層に上手く分かれたとしても、各層には4〜5名しかいないことになりますね。これでは統計処理の精度が下がってしまいます。
このようにデータが細かく分かれすぎてしまい、各層に十分なサンプル数が確保できなくなることを「層化の呪い」や「次元の呪い」と呼びます。上記の様な理由で、交絡因子が複数ある場合のように複雑なデータを扱う場合には標準化による対処が難しくなってしまいます。
そのため、実際には回帰モデルや逆確率重み付け(IPW) といった手法を用いて交絡因子に対処していくことになります。
おわりに
代表的な交絡調整の手法である標準化について解説してきました。
終盤の説明では標準化の限界にも触れたため、「せっかく勉強したのに、標準化は使わない手法なの?」と落胆した方もいるかもしれませんが、決してそうではありません。
冒頭の説明でも述べているように、標準化について理解を深めることは、これまで学んできた因果推論の考え方に基づき「いざ、因果推論を実践する」ための土台を作ることでもあります。
この記事を最後まで読んでいただき、標準化の考え方を大まかにでも理解した皆さんは「交絡因子を、標準化等の手法によって調整し、 Exchangeabilityを保証する」という因果推論の根幹を担う考え方がすでに身についているはずです。
これから因果推論の学習を進めていく中で、参考書や論文で難解な分析手法に出会うかもしれませんが、ひとまずは「交絡因子を調整して、Exchangeabilityを成り立たせたいんだな」と割り切って前に進む事もできるでしょう。
また、解説の途中においてはConsistencyやExchangeability、Randomizationといった用語を意図的に繰り返してきましたので、これまでmMEDICI Libraryで学んできた知識が知らず知らずのうちに定着しているはずです。
次の記事では、交絡調整の代表的な手法のひとつである逆確率重み付け(IPW)について解説していきます。引き続き、因果推論の学びを深めていきましょう。
参考文献
ウェブサイト
KRSK.データから因果関係をどう導く?:統計的因果推論の基本、「反事実モデル」をゼロから.(https://www.krsk-phs.com/entry/counterfactual_assumptions)
参考図書:『Causal Inference: What If』
Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。
mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。
因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。
そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。
mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンズホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。
本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです!
・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ(ex. RWDピア)
・24時間利用可能なオンライン自習室「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください!
・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催【YouTubeラジオコンテンツ 耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。
すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。
シリーズ一覧
シリーズ紹介|ゼロから学ぶ因果推論
「医学研究は難しい」、きっと多くの方がそう感じているでしょう。
因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。
因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。
「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。
因果推論シリーズ
vol.1:因果推論の出発点 - 因果と関連の違いとは? -
vol.2:因果効果の基本を徹底解説 - Individual Causal Effect(個人因果効果)とAverage Causal Effect(平均因果効果)の違いとは? -
vol.3:初心者のためのTarget Trial Emulation(TTE)
- Part 1 ; ETAFOCAフレームワークについて
- Part 2 ; 三つの時点で考えるバイアスとその対処法
- Part 3 ; 論文の実例で理解を深めるTTEvol.4:Exchangeability(交換可能性)を徹底解説 - Randomization(ランダム化)が実現する因果推論の必須条件 -
vol.5:Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.6:Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.7:Consistency(一致性)を徹底解説 - 観測データと反事実アウトカムを一致させよ -
vol.8:Positivity(正値性)を徹底解説 - 因果推論の落とし穴を回避せよ -
vol.9:Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
vol.10:効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか? -
vol.11:交互作用を徹底解説 - 複数の介入による相乗効果 -
vol.12:DAGを徹底解説
vol.13:交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
vol.14:選択バイアスを徹底解説 - 消えた患者が結果を歪める?-
©mMEDICI Inc. ALL RIGHTS RESERVED.



















