【疫学専門家監修】DAGを徹底解説 | 応用編：調整してはならない？コライダーと媒介変数の落とし穴 - ゼロから学ぶ因果推論 vol.12-2

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに

DAGを徹底解説（応用編）では、DAGを用いて因果推論の理解をさらに深めるために、「コライダー」や「媒介変数」といったバイアスの原因となりうる変数に焦点を当てて解説します。

これらの変数は、誤って調整してしまうと因果効果の推定を歪める要因となるため、DAGを使ってその構造を正しく捉えることが重要です。

本記事では、具体例やDAGを交えながら直感的に理解できるよう丁寧に説明しています。

※DAGの基本（構成要素やバックドアパス、交絡など）については前編（DAGの基礎編）で解説していますので、未読の方はそちらから読み進めていただくことをおすすめします。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• コライダーの定義とDAGによる表記

• 媒介変数の定義とDAGによる表記

• DAGにおける注意点

この記事は誰に向けて書かれているか

• DAGについて詳しく学びたい方

• コライダーや媒介変数について理解したい方

• DAGを読み解けるようになりたい方

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

執筆者の紹介

氏名：松下翔
所属：橋本市民病院総合内科
自己紹介：東京大学医学部を卒業後、天理よろづ相談所病院で初期研修・後期研修 (内科ローテートプログラム)を行い、内科専門医を取得。その後、京都大学公衆衛生大学院 医療疫学教室博士後期課程に進学。現在は橋本市民病院総合内科フェローとして常勤で臨床を続けながら、社会人大学院生として疫学を学んでいる。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。

後編（応用編）に入る前に

前編（基礎編）では、DAGの構成要素やバックドアパスについて学び、交絡因子を視覚的に整理して適切に調整する方法を学びました。

後編（応用編）では、因果推論における重要な変数である「コライダー」や「媒介変数」についてDAGを用いながら理解を深めていきましょう。

1．コライダーとは？

まずは「コライダー（collider）」についてご説明します。

コライダーとは、曝露とアウトカムの「共通の結果」となる変数のことで、「合流点」とも呼ばれます。

"collide"は英語で「衝突する」という意味であり、２本の矢印の先端（矢頭）が一つの点に向かって「ぶつかる」構造を指して「コライダー」と呼ばれます。

コライダーは、交絡因子と比較してなじみが少ない方が多いのではないでしょうか？

コライダーは直感的に理解することが難しい概念ですが、因果推論において非常に重要な概念です。

なぜなら、交絡因子とは逆に「調整してはいけない」変数であり、誤ってコライダーを調整すると、新たなバイアス（とくに選択バイアス）が生じてしまうからです。

それでは、コライダーについて、一つ一つ理解していきましょう。

コライダーの定義

コライダーとは、DAGにおいてニつ以上の変数（ノード）からの矢印が合流し、「共通の結果」となる変数のことです。

Sに向かってニつの矢頭が合流しているため、Sをコライダーと呼びます。

交絡因子の経路（X ← C → Y）は共通の原因（common cause）を示しましたが、コライダーの経路（X → S ← Y）は共通の効果（common effect）を示します。

この時、XとYの間の経路（X → S ← Y）は、DAG上では「パスが閉じている」状態です。つまり、XとYには関連がない状態にあります。

Sで条件付けるとパスが開くことになります。その結果、XとYに本来は存在しないはずの「見かけ上の関連」が生まれ、因果推論におけるバイアスをもたらすことになります。これこそが、コライダーが「調整してはいけない変数」である理由です。

以下の解説を通じて、コライダーについてより具体的に考えていきましょう。

コライダーの具体例

コライダーについて、身近な具体例を用いて考えてみましょう。

例えば、ある高校では「筆記試験（学力）」と「スポーツ選抜（運動能力）」のニつの方法で入学試験を実施しているとします。

この場合、「入学試験への合格」は「学力」と「運動能力」の共通の結果、すなわちコライダーです。

通常、「学力」と「運動能力」には直接的な因果関係はありません。
つまり、勉強ができるからといって運動が得意とは限らず、逆もまた然りです。

しかし、入学試験に合格した生徒だけを対象にすると「学力」と「運動能力」の間に関連（負の相関関係）が生じてしまいます。

その理由を紐解いていきましょう。

コライダーが生み出す「見せかけの相関」

この高校に入学するためには ① 学力が高い（筆記試験で合格） ② 運動能力が高い（スポーツ選抜で合格） のどちらか、または両方の条件を満たす必要があります。

学力が低くても合格できた人は、どんな人でしょうか。
そうです、運動能力が高く、スポーツ選抜で合格した人ですよね。


逆に、運動能力が低くても合格できた人は、どんな人でしょうか。
そうです、学力が高く、筆記試験で合格した人ですね。

その結果、合格者は以下のような傾向をもつことになります。

学力が高い人は、運動能力が低い傾向がある
運動能力が高い人は、学力が低い傾向がある

合格者だけを見て「学力」と「運動能力」の関係を推定することは「入学試験に合格した」という条件を揃えて比較していることになりますね。

つまり「合格」というコライダーで条件付けしていることになります。

コライダーで条件付けることによって、本来関連がないはずの「学力」と「運動能力」に関連（負の相関関係）が生じてしまうのです。つまり、DAG上で「XとYのパスが開く」状態になります。

また、このように「入学試験の合格者」といった特定の集団を選択的に対象とすることによって生じる系統的な偏りを「選択バイアス（selection bias）」と呼びます。コライダーを調整することは、選択バイアスを生じさせる要因の一つです。

コライダーのまとめ

• コライダーを通る経路は、コライダーで条件付けることで開く

• コライダーで条件付けることで、選択バイアスが生じる

• そのため、コライダーは調整してはいけない変数である

適切な因果推論を実践するために、これらルールをしっかりと覚えておきましょう。

2． 媒介変数とは？

媒介変数とは「暴露（X）」が「アウトカム（Y）」に影響を与える途中にある変数です。

つまり「XがYに直接的に影響を与えるのではなく、Mという変数を介して影響を与えている」という場合、M（中間因子）が媒介変数になります。

媒介変数と交絡因子を混同してしまう方もいるかも知れません。
ここで注意しなければならないことは、媒介変数と交絡因子は異なる性質をもつ変数であり、交絡因子は「調整すべき変数」でしたが、媒介変数は「調整してはいけない変数」です。

まずは媒介変数と交絡因子との違いを理解しながら、媒介変数について理解を深めていきましょう。

媒介変数と交絡因子の違い

媒介変数の定義は、曝露（X）がアウトカム（Y）に影響を与える途中にある変数のことです。

DAGではX → M → Yと示されます。

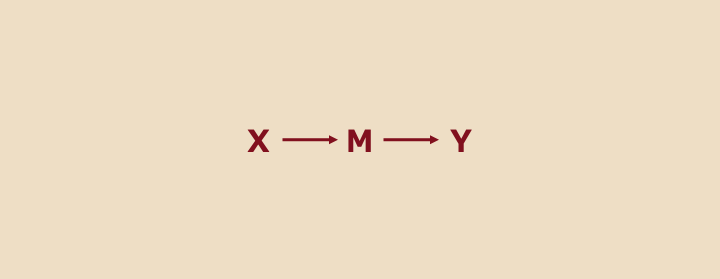
媒介変数を介した有向経路は、自然には開いています。つまり、XとYに関連がみられます。

Mで調整してしまうと、XとYの間の関連は消えてしまいます。

XがMを介してYに与える影響をみたかったにもかかわらず、関連が消えてしまうため、媒介変数Mで調整してはいけません。

※より正確には、媒介変数で調整することもあります。
「XがYに与える媒介変数Mを介さない効果を推定したい」というモチベーションでMを調整することはあります。しかし、XがYに与える全体の効果（marginalな効果）を見たい時には、Mで調整すると関係が薄まってしまいます。

一方、交絡因子の定義は「曝露（X）」と「アウトカム（Y）」の「共通の原因」でしたね。
DAGではX ← C → Yと示されます。

交絡因子を介したバックドアパスもまた、自然には開いています。
つまり、XとYの間に因果関係がなくても、交絡因子Cを介した経路によって関連がみられます。

このようにXとYの間に「見かけ上の関係」が生じてしまうため、交絡因子Cは調整しなければならない変数と言えます。Cで調整することで、XとYの間のバックドアパスを「閉じる」ことができます。

バックドアパスと交絡の関係：
DAGを徹底解説（基礎編）- 因果推論の必須ツールで交絡因子を可視化する - ゼロから学ぶ因果推論 vol12-1 

媒介変数の具体例

例えば「運動」が「心疾患リスク」を低下させる効果を調べたいとします。

運動の影響は多面的で、「血圧の改善」や「メンタルヘルスの向上」など、複数の経路を通じて心疾患リスクに影響を与えると考えられます。

ここではシンプルな仮定として「運動が血圧を下げる」→「血圧が下がることで心疾患リスクが低下する」というメカニズムに注目します。

この時「血圧」は 運動（X）と心疾患リスク（Y）の媒介変数（M）として扱われます。

※運動による血圧低下以外の作用（例: メンタルヘルスの向上）を介して心疾患リスク低下に至る経路は考慮していません。


「運動が心疾患リスク低下に与える全体の効果」を見たい時に、同じ血圧の人で比べてしまう（血圧で条件付ける）と、「全体の効果」から「運動が血圧への影響を介して心疾患リスクを低下させる効果」を除外することになってしまいます。

結果として「運動が心疾患リスク低下に与える全体の効果」を過小評価してしまうかもしれません。


このように、媒介変数を調整することで、本当に知りたい因果効果の推定を歪めてしまうことになるため注意する必要があります。

3．交絡因子・コライダー・媒介変数のまとめ

ここまで、交絡因子・コライダー・媒介変数について説明してきました。
それぞれの変数について、表にまとめて整理しましょう。

医学研究においてよくある誤解に「たくさんの変数を調整すればするほど、精度が高い結果が得られる」というものがありますが、ここまでの説明を踏まえるとその考えが間違いであることがよくわかりますね。

DAGを用いて「交絡因子」「コライダー」「媒介変数」といった変数を明確に整理し、交絡因子に対する調整や、コライダー・媒介変数を見誤って調整しないように注意することで、より正確な因果推論の実現につながることでしょう。

調整・条件付けとは？

ここまでの説明で「調整」や「条件付け」という用語が何度も登場しました。なんとなく意味はお分かりの方が多いと思いますが、ここで少し整理しておきましょう。

「調整（Adjustment）」とは、X（暴露）とY（アウトカム）の関係を明らかにするために、他の要因の影響を取り除くことを指します。

調整には層別化、逆確率重み付け、マッチング、標準化などの手法があります。

中でも、他の条件を固定して（他の条件が同じだったと仮定して） XとYの関係を推定することを「条件付け（conditioning）」と言います。

たとえば、「たばこ」と「肺癌」の関係を調べたいとしましょう。 一般に、年齢が高いほど喫煙者が多く、また年齢が高いほど肺がんのリスクも高くなります。

このように、「年齢」が「暴露（たばこ）」と「アウトカム（肺癌）」の両方に影響しているとき、「年齢が同じだったと仮定した時に、たばこと肺癌の関係はどうなるか？」を考えるのが、条件付けです。

つまり、「たばこ」と「肺がん」の関係に影響を与える条件を揃えて比較するということです。

具体的には「同じ年齢層の人」で「喫煙」と「肺がん」の関係を見る、あるいは年齢を変数として加えた回帰モデルで喫煙と肺がんの関係を推定するといった方法が挙げられます。これらはいずれも「条件付け」に該当します。

4．DAGの注意点

前編からここまでにかけての説明で、DAGが因果推論を実践するために必須なツールであることがご理解いただけたと思います。

そんなDAGにもいくつかの注意点があるためご紹介します。


① DAGで描かれる関係はあくまで研究者が想定した仮定である
DAGは研究者がドメイン知識を活用して変数間の因果関係を想定して書きます。

現実世界の複雑な因果関係を単純化することになるため、研究者によって想定するDAGは異なることがあります。唯一絶対の正しいDAGは存在しません。

このため、複数の研究者で議論し、DAGに描かれていないが重要な交絡因子がないか、未測定の交絡因子の影響をどう考えるか、など議論する必要があります。


むしろ、DAGを書くではじめて明確な仮定を共有することができ、議論を深めることができるのです。


② 因果の方向や大きさを表すことはできない
DAGは定性的なグラフであり、影響が正の方向なのか、負の方向なのか、あるいはどの程度なのか（量的関係）ということを表現することができません。


③ 双方向に影響する関係を表現するときに、グラフが複雑になる
さらに、DAGは非巡回という性質を持ちますが、実際には双方向に関係しているように思える因果関係を見たい時もあります。

その際は時間を概念に含めることで、DAGに表現できますが、かなり複雑になります。


例えば、「運動することで体重が減り、体重が減るとさらに動きやすくなって運動量が増える」という関係を表現したいとき、時間の因子を考慮することで、

ベースラインの運動習慣　→ 　１か月後の体重変化　→ 　２か月後の運動習慣

というように、非巡回の性質を保ちながら双方向の関係を示すことができます。


ただし、それぞれに交絡する要因など考えていくと全体としてのDAGがかなり複雑になってしまうという限界があります。


④ 効果修飾や交互作用を表現することが難しい
また、DAGの限界として、効果修飾や交互作用をDAGで表現することが難しい点も挙げられます。

効果修飾や交互作用については、下記の記事をご参照ください。

【疫学専門家監修】効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ - ゼロから学ぶ因果推論 vol.10

【疫学専門家監修】交互作用を徹底解説 - 複数の介入による相乗効果 - ゼロから学ぶ因果推論 vol.11

5．DAGの書き方

最後に、実際にDAGを書くためのステップをご紹介します。

この時、紙にボールペンで書くと一番練習になりますが、パソコンでもDagittyというソフトウェアで描くことができます。


DAGの書き方は四つのステップからなります。

① 関心のある曝露とアウトカムを設定する。
② ドメイン知識を用いて、曝露またはアウトカムに影響を与えうる変数を全て書き出す。
（実際には測定できない変数も書き出すことが推奨されています）
③ 変数間に因果関係があると考えられる場合、矢印で線を引く。
④ 複数の研究者で協議し、DAGを修正する。


実際に手を動かしてDAGを書いてみると、より理解が深まると思います。

DAGの限界を踏まえながら、上手に活用することで、因果推論の仮定を明確に整理し、活発に議論することができるようになるでしょう！

6．まとめ

前編と後編に分けてDAGについて解説してきました。

前編ではDAGの基本やバックドアパスと交絡について学び、後編ではコライダーや媒介変数といった概念についてDAGを用いて理解を深めてきました。

DAGを用いることで交絡因子を見極め、調整すべき変数・してはいけない変数を判断し、そして因果推論の仮定を明示することが論理的に行えるようになります。

複雑な因果構造を整理し、そして適切に因果推論を実践するためにDAGは必須のツールです。

この解説が、みなさんの臨床研究や疫学研究における因果推論の理解と実践に役立てば幸いです。

DAGを徹底解説（基礎編）- 因果推論の必須ツールで交絡因子を可視化する - ゼロから学ぶ因果推論 vol12-1 

参考文献

• 井上浩輔．医学研究のための因果推論レクチャー．医学書院2024

• 鈴木越治．医学における因果推論 第5部．日本衛生学雑誌 2009年64巻4号p.796-805．doi:https://doi.org/10.1265/jjh.64.796

• Digitale JC, Martin JN, Glymour MM. Tutorial on directed acyclic graphs. J Clin Epidemiol. 2022;142:264-267. doi:10.1016/j.jclinepi.2021.08.001

• Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999;10(1):37-48.

• Lipsky AM, Greenland S. Causal Directed Acyclic Graphs. JAMA. 2022;327(11):1083-1084. doi:10.1001/jama.2022.1816

• Feeney T, Hartwig FP, Davies NM. How to use directed acyclic graphs: guide for clinical researchers. BMJ. 2025;388:e078226. doi:10.1136/bmj-2023-078226

• "矢印"をつかって因果関係を視覚的に整理する：因果ダイアグラム（DAG)入門①〜なぜDAGが必要なのか〜https://www.krsk-phs.com/entry/DAG1

参考図書：『Causal Inference: What If』

Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。

mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。

そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。

mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る｜ 無料体験に申し込む

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する

  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？-