【医師執筆＆疫学専門家監修】因果推論の出発点 - 因果と関連の違いとは？ - ゼロから学ぶ因果推論 vol.1

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに 

原因と結果の関係を科学的に解き明かす「因果推論」。医療現場でよく耳にするこの言葉、実は「関連」とは異なる概念です。

この記事では、因果推論の基礎となる「因果（Causation）」と「関連（Association）」の違いを、具体的な例を交えてわかりやすく解説します。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• あなたも「因果」や「関連」ということばを聞いたことがあるかと思います。でも、いざこのふたつの違いについて正確に説明しようとすると、あれ？と感じませんか？

• 因果推論という考え方では、このふたつの違いがわかり意識することが第一歩になる、といえるでしょう。

• 本記事ではこのふたつの違いについて説明していきますが、統計の専門用語や数式がわからなくても安心してください。

• はじめての方でもこの記事を最後まで読めば、ご自身でPr[Ya=1=1] ≠ Pr[Ya=0=1]、Pr[Y=1|A=1] ≠ Pr[Y=1|A=0] というふたつの数式をつかってCausation（因果）とAssociation（関連）の違いを説明できるようになるはずです！

この記事は誰に向けて書いているか

• CausationやAssociationという文字と先の数式をみて、読むのをやめようと思った方

• 臨床研究や論文で、難解な統計や数式がでてきて挫折した方

• 「因果推論」という言葉を聞いたことがあるけどよくわからないという方 

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

執筆者の紹介

氏名：早坂美紗
所属：Research Fellow, Maternal Fetal Medicine, Department of Obstetrics & Gynecology EVMS at Old Dominion University
経歴：道北での産婦人科診療に8年間従事、2024年7月より現職。産婦人科専門医、女性のヘルスケアプロバイダー、がん治療認定医。現在は産婦人科領域を中心とした環境・社会要因と医療格差を主なテーマに日米のデータベースを用いた研究に取り組んでいる。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人が格差を超えてアクセス可能な一流の知のプラットフォームによって「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。 

CausationとAssociationの違いがわかると、こんなことができる！

Causation （因果） と Association （関連） は一見すると似ていますが、全く異なる概念です。この違いを理解することは、適切に「因果推論（Causal Inference）」を行っていくために必須です。

なぜ違いを知る必要があるのか？

このふたつを混同してしまうと、どんな困ったことが起こるでしょうか？例えば、以下のような根拠と意思決定の関連についてどう思いますか？

根拠：がんになった人の多くは痛み止めを使っている
意思決定：がんを予防するために痛み止めの使用をやめよう！

根拠：コウノトリの数が多い国では出生数が高い
意思決定：少子化を食い止めるため、コウノトリの繁殖に力をいれよう！

根拠：警察官が多い地域では犯罪率が高い
意思決定：警察官の数を減らせば犯罪が少なくなるはずだ！

いずれも何かおかしいな、と感じるはずです。これらの例ではAssociation（関連）を、誤ってCausation（因果）ととらえてしまったことにより、意思決定のおいて大きな失敗を犯してしまっています。

これほど極端でなくても、日常において病気の治療や予防のたえの介入、様々な政策決定において、関連と因果を取り違えた結果として不適切な意思決定をしてしまう恐れがあります。そのため関連・因果は明確に区別する必要があり、簡潔に言えば以下のように定義されます。

Causation（因果）とは「原因と結果」にあたると考えると理解しやすいかもしれません。原因となる一方を変化させた場合（例えば治療などの介入）、結果となる他方が必ず変化する（疾患の治癒率など）、このとき両者には因果関係があるといえるでしょう。


一方で、Association（関連）は、ある2つの事柄に「なんらかの関係」がみられる状態を指します。

因果関係と異なり、この2つの事柄の間には、原因と結果のように順序がない場合や、常に同じ関係が成り立たない場合、またほかの要素が関係に影響を与えている場合、なども含まれます。

例えば、「アイスクリームの売上が増えると熱中症が増える」という関連が観察されることがありますが（暑い季節になるとアイスクリームが売れ、かつ熱中症になる人が増えるから）、これを知って「アイスクリームが売れたせいで熱中症が増える！」と思う方はいないでしょう。

つまり、みなさんは「因果と関連の違い」を既に直感的に理解しているということです。

このように、因果と関連とは全く別の現象であり、論文を読み書きする上では明確に区別できなければなりません。

ではこれから関連と因果の違いを深掘りしていきますが、まずはそれを知るために必要なIndividual Causal Effect（個別因果効果）とAverage Causal Effect（平均因果効果）について説明していきます。

Individual Causal EffectとAverage Causal Effect

Individual Causal Effect（個別因果効果）とは？

たとえば治療Aに病気Yを治す効果があるのかを知りたいとしましょう。

治療：1月1日にスズキさんが治療Aをうけました
効果：1月5日に病気Yが治りました

この情報からスズキさんにとって治療Aは病気Yを治すのに効果があった、といえるでしょうか？

一見すると「言える」と思うかもしれませんが、実はこの情報だけでは治療Aの効果を判断することはできません。

なぜならば、「スズキさんは治療Aをうけなくてももともと病気Yが治っていた」という仮説に対し、上の情報だけでは反論ができないからです。

そのため、スズキさんにとって「治療Aが病気Yを治すのに効果があった」というためには以下の2つの仮定が満たされなくてはなりません。

仮定①
治療：1月1日にスズキさんがある治療Aをうけました
効果：1月5日に病気Yが治りました

仮定②
治療：1月1日にスズキさんがある治療Aをうけませんでした
効果：1月5日に病気Yが治りませんでした

仮定①と②が成立すれば、それぞれの違いは「治療Aをうけたかどうか」以外にはありませんから、「治療Yが治ったかどうか」という効果は治療Aの有無にもたらされたと判断することができます。

しかしながら、スズキさんという個人においてこの2つの仮定の双方を現実世界で観測することは不可能です。

そのためにはタイムマシンで時を戻し、スズキさんが治療Aをうけた場合とうけなかった場合の2つの現実を観測することしかできませんが、タイムマシンは存在しませんので「治療Aをうけた」現実を観測した場合、「治療Aをうけなかった」という現実は永遠に観測不可能となります。

そのため、Individual Causal Effect（個別因果効果）を現実世界で測定することは不可能です。

Average Causal Effect（平均因果効果）とは？

Individual Causal Effect（個別因果効果）が個人における因果効果を考えていたのに対し、それを集団に拡張したものがAverage Causal Effect（平均因果効果）です。

なぜ平均かというと、集団において治療を受けた時と受けなかった時それぞれの平均的な効果を測定するからですね（例えば10人中5人が治癒した場合の治療効果は50%のように）。

Causation（因果）とAssociation（関連）の違いとは

では、ここまでの話を踏まえてこの記事の本題であるCausation（因果）とAssociation（関連）の違いを考えていきましょう。 

Causation（因果）とは

以下のような記号を用います。

治療Aをうける：a=1
治療Aをうけない：a=0
※Aが小文字になっているのは、後述する反実仮想における話だからだ、とここでは理解してください

治療Aをうけた場合の5日後の病気の状態：Y^{a=1}
治療Aをうけなかった場合の5日後の病気Yの状態：Y^{a=0}

病気Yが治った場合：Y＝1
病気が治っていない場合：Y＝０

すると、集団において全ての人が治療Aをうけた場合、うけなかった場合、それぞれの結果は次のようになります。

（なお個別因果効果と同様に、集団においてもタイムマシンを使って「全員が治療をうけた場合」と「全員が治療をうけなかった場合」の双方を観察することは不可能ですので、これはあくまでも仮想世界におけるシミュレーションであり、これを反実仮想と呼びます）

これをもとに、全ての人が治療Aをうけた場合と全ての人が治療Aをうけなかった場合でそれぞれ病気Yが治る確率（Probability）を考えます。

すべての人が治療Aをうけた場合（a=1）の病気Yが治る（Y=1）確率：Pr[Y^{a=1}=1]
すべての人が治療Aをうけなかった場合（a=0）の病気Yが治る（Y=1）確率：Pr[Y^{a=0}=1]

と表すことができます。なお、PrとはProbabilityに由来し、確率の表記です。

上の例では次のような結果となりました。

Pr[Y^{a=1}=1 = 5/7
Pr[Y^{a=0}=1] = 2/7

以上の結果より、Pr[Y^{a=1}=1] ≠ Pr[Y^{a=0}=1]　が成り立ち、この時に「平均因果効果（Causal Effectがある）」とされます。

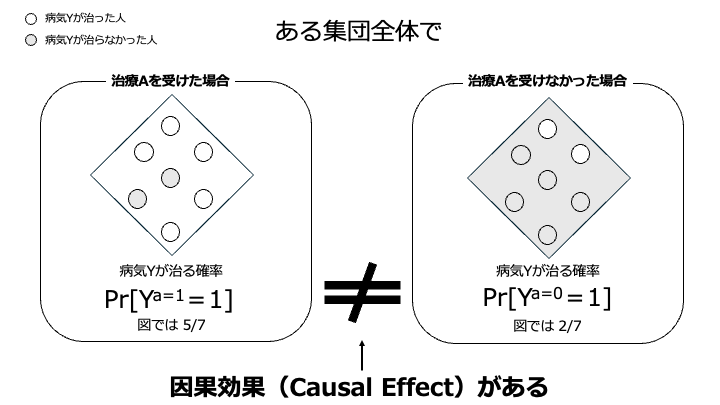
全ての人が治療Aをうけた場合と、全ての人が治療Aをうけなかった場合で病気の治癒の有無が変わったとすると、それは治療Aの有無以外には差分はないわけですから、「治癒の有無は、治療Aの有無によってもたらされた」と言えるわけです。

Association（関連）とは

しかしながら、既に説明したようにタイムマシンのない現実世界においては同一の集団において「全ての人が治療Aをうけた場合と全ての人が治療Aをうけなかった場合」の双方を観測することは不可能です。

ではどうするかというとAverage Causal Effect（平均因果効果）に着目し、集団において「治療を受けた人」と「治療を受けなかった人」の結果をそれぞれ測定し、比べるのです

以下の図の左側でやっていることですね。 

Causationの図では、反実仮想としてそれぞれの個人において治療をうけた場合（Y^{a=1}）と治療をうけなかった場合（Y^{a=0}）の双方のアウトカムが並列されていました。

しかしながら、タイムマシンが存在しない現実世界では個人は「治療を受けた」か「治療を受けなかったか」のいずれかにしかなれないため、観測できるアウトカムも片方のみとなります。


ではこの集団における病気Yが治る（Y=1）確率Pr、はどのように表すことができるでしょうか？

治療Aをうけた人における病気Yが治る確率：Pr[Y=1|A=1]
治療Aをうけなかった人における病気Yが治る確率：Pr[Y=1|A=0]

 
反実仮想では治療Aが小文字aで表されていたのに対し、今回は大文字で表されていますが、これは「現実世界の話だから」とここでは理解してください。

そして、[Y=1|A=0]の”|”は「ある集団においてA=0の人たち」であることを意味し（つまり治療を受けなかった人たち）、これを専門用語で“A=0で条件づける”と言います。

さて、では実際に病気Yが治る（Y=1）確率Prを計算すると以下のようになります。

Pr[Y=1|A=1] = 3/4
Pr[Y=1|A=0] = 1/ 3

このように、Pr[Y=1|A=1] ≠ Pr[Y=1|A=０]　が成り立つ時、

治療Aと病気Yの間にはAssociation（関連）があるということができます。

Associationを図に表すとこうです。

Causation（因果）とAssociation（関連）の違い

Causation（因果）効果がある、というときには
Pr[Y^{a=1}=1] ≠ Pr[Y^{a=0}=1] が成り立ち（これは反実仮想の話）、

Association（関連）がある、というときには
Pr[Y=1|A=1] ≠ Pr[Y=1|A=0] が成り立ちます（これは現実世界で観察できる）。

そして、既に説明した通り我々が実際に観測できるのはAssociationであり、タイムマシンが誕生しない限りはCausationは観測不可能です。

とすると読者の皆さんは「え、じゃあCausationって絶対に判定できないの？」と思われるでしょう。

そこで登場するのがこのシリーズ記事のトピックであるCausal Inference（因果推論）です。

Causal Inference（因果推論）では、つまり実際に観察できるAssociation（関連）から、Causation（因果）を推測する手段を学びます。

数式で言うならば、

Pr[Y=1|A=1] ≠ Pr[Y=1|A=0]の式を、Pr[Y^{a=1}=1] ≠ Pr[Y^{a=0}=1]に近似させる手段を学ぶ

と言うことです。

この近似がいかなる時に成立すると言えるのか、これから本シリーズ記事ではその方法を一つずつ丁寧に解説していきますので、ぜひお楽しみください。

まとめ

この記事ではCausation（因果）と Association（関連）の違いについて説明してきました。

科学的思考の根拠となる因果推論の第一歩として、このふたつの違いを理解することで、いままで難しく感じていた研究デザインや統計解析の手法について、そういうことだったのか！と感じることが増えていくはずです。

参考図書：『Causal Inference: What If』

Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。

mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。

そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンズホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？-