【疫学専門家監修】Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）により実現する因果推論の必須条件 - ゼロから学ぶ因果推論 vol.4

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに

突然ですが、「なぜランダム化比較試験（RCT）からはエビデンスレベルの高い結果が得やすいんですか？」と聞かれ、クリアに回答できるでしょうか？

医学研究を学んだことがある方であれば、「RCTはエビデンスレベルが高い」というセリフを一度は耳にしたことがあるでしょう（厳密に言えば、”適切にデザインされたRCTは”ですが）。

しかし、「なぜ？」と聞かれて因果推論の観点からクリアな説明ができる方は、実はあまり多くないかもしれません。

この記事では、「RCTとはどんなデザインで、そしてそのデザインによってなぜ頑健な因果推論が可能になるか」ということを学術的に語れるようになるために必要なランダム化（Randomization）と交換可能性（Exchangeability）という重要な概念を解説します。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• なぜRandomizationにより頑健な因果推論が可能となるかが説明できるようになる

• Exchangeabilityの意味、因果推論における必要性について説明できるようになる

• Ideal randomizationとConditional randomizationの違いと注意点を説明できるようになる

この記事は誰に向けて書いているか

• 複雑な数式が苦手だが因果推論の基本を学びたい方

• 医学研究のゴールドスタンダードであるRCTについて理解を深めたい方

• 因果推論に興味はあるが既存のブログでは難しく挫折した経験がある方

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

執筆者

氏名：木下大士
所属：病院勤務（理学療法士）
専門性：大学卒業後より急性期総合病院で理学療法士として臨床業務に従事。医療現場に留まらない幅広いフィールドで人々のHealthに関わりたいと考え、パブリックヘルスを学ぶことを決意。2025年度より東大SPH進学予定。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。

Causation と Association の架け橋を作る

因果推論シリーズ記事のVol.1で説明されている通り、Causation（因果）は現実世界では直接的に求めることが出来ません。

なので、現実世界で求めることができるAssociation（関連）から、Causation（因果）を推論するためにCausal Inference（因果推論）を行う必要があります。

そのための手法として、この記事ではRandomizationについて学んでいきましょう。

因果推論とRCT

こちらの図は医学界における研究デザインごとのエビデンスの強さを示したもので、エビデンスピラミッドと呼ばれます。

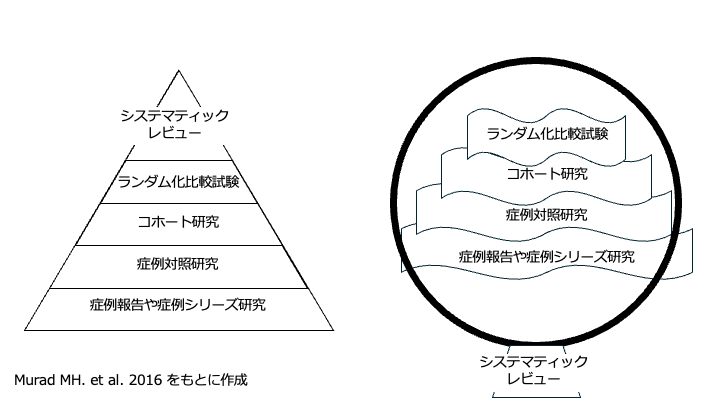
古典的には左図、近年は右図が用いられるています。

この図の「ランダム化比較試験」がRCTに該当します。

ここから分かるように（適切にデザインされた）RCTは単一の研究では最も頑健なエビデンスを提供する研究デザインだと考えられています。

”頑健な”とは専門用語を使って解説すると”内的妥当性が高い”状態であり、これはつまりバイアスの影響を抑えてAssociationからCausationをより正しく推論できるということを意味します。

そして、RCTがエビデンスピラミッドにおいて単一の研究として最上位に位置付けられている主な理由が、今回解説する”Randomization” という取り組みと、それにより理論的に実現される ”Exchangeability”にあります。

この記事では、”Randomization” と ”Exchangeability”を詳しく解説し、「なぜ（適切にデザインされた）RCTが頑健なエビデンスを提示すると言えるのか」ということを因果推論の文脈で考えていきましょう。

“Randomization” と “Exchangeability”

Randomizationとは

Randomizationは直訳すると”無作為化”という意味になります。

つまり、試験の対象集団に対して介入の有無をコイントスのようにランダムに（無作為に）割り付けることを意味しています。 

薬の効果を明らかにするための治験ではスタンダードに使用される手法ですが、製薬企業はこのRandomizaitonを行うために数十億から数百億の費用をかけることもあります。

なぜこれだけ莫大な費用をかけてまでRandomizaitonをするのでしょうか？

Randomizaitonなしに現場の医師が「あなたは薬Aね」というふうに思い思いに割り振るだけではいけないのでしょうか？

それは以下の理由です。

Randomization（無作為化）によって2群間の交絡因子の分布をバランシングし、Exchangeabilityを実現するため

Ideal randomized experimentとは

さて、ここまでで「なるほど、RCTをやるのはExchangeabilitなるものを実現するのが大きな目的なんだな」ということを理解頂けたかと思います。

「いきなり知らん言葉がでてきたぞ」と驚いたかもしれませんが、しっかりと解説していくのでご安心ください。

ここからはExchangeabilityについて考えていくのですが、その前にExchangeabilityを考えるにおいてRCTの重要な仮定としてIdeal randomized experimentの解説をします。

Ideal randomized experimentでは「全ての人がフォローアップがされ、治療に対するアドヒアランスが完全で、治療内容が統一され、二重盲検化されている」と仮定されています。

なぜこのような仮定を置くかと言うと、実は今回着目しているExchangeabilityが実現できたとしても、それだけではAssociationからCausationを推論するには不十分だからです。


例えば、患者が割り付けた治療から脱落してしまう、割り付けた治療の定義が不十分で治療内容にばらつきが出る、アウトカムの判定者が割り付け内容を知っており判定が歪む、といった状況が起こると、RCTにおいても頑健な因果推論が妨げられてしまいます。

しかしながら、こうしてあれもこれもと条件を考えていても混乱してしまいますので、まずは因果推論における核となる概念であるExchangeabilityを理解するために、「それ以外の条件は完璧に達成できている」という仮定を置きましょう。

これがIdeal randomized experimentです。

Exchangeabilityについて

Exchangeabilityは直訳すると”交換可能性”という意味になります。
馴染みのない言葉ですが一つずつ紐解いていきましょう。

Exchangeabilityとは？

Exchangeabilityとは、「介入群と対照群の割り当てを交換したとしても、得られる結果が同じである」ということを意味します。

「何をいってるのか分からん」という気持ちになったと思いますが、丁寧に解説していきますのでご安心ください。

図で説明しましょう。

抗がん剤治療が生存率に与える影響を調べるため、RCTでひし形の対象集団にランダムに治療あり・なしを割り付けたとします。

その結果、白部分の人たちは治療ありとなり、グレー部分の人たちは治療なしとなりました（左図：条件A）。

そして、生存率は治療あり群が50%、治療なし群が20%でした。

この時、タイムマシンで時を戻して、治療を割り付けを逆にしたら生存率はどうなると思いますか？

つまり、白部分の人たちには治療なしを、グレー部分の人たちには治療ありを割り付けるということです（右図：条件B）。


さて、この時に条件A・条件Bでそれぞれの群の生存率は変わるでしょうか？

直感的に「変わらない」と判断することができるかと思います。

治療あり・なしはランダムに割り振られていますから、条件Aにおいて治療ありの群の生存率が50%だったのに、条件Bでは治療ありの死亡率が30%になる、とは考えにくいですよね？

なぜこのようなことが実現できるかというと、ランダム化によって治療あり・なしの2群間の交絡因子が平均的には同質に揃えられているからです。


例えば癌のステージは今回の研究では交絡因子となりますが、ランダム化によって両群のステージもバランシングされています（つまりステージが交絡していない）。


これがExchangeabilityが実現されている状況です。

Exchangeabilityが実現できない状況

一方で、ランダム化を行わずに観察データを用いた場合はこのような条件は成立させられません。

例えば抗がん剤の生存率への影響を調べるために、とある病院においてがん患者の電子カルテを集めたとしましょう。

そして、抗がん剤を使っていた患者を抗がん剤群に、使っていなかった患者を非抗がん剤群として扱います。

その結果、抗がん剤群の生存率は20%、非抗がん剤群のそれは50%でした。


では、タイムマシンで時を戻して「先ほど抗がん剤群だった患者にはやはり抗がん剤を使用せず、先ほど非抗がん剤群だった患者には抗がん剤を使用した」とします。

この時、RCTで観察されたように「治療の割付を交換しても、結果は同じ」になるでしょうか？

なりませんよね？

なぜなら、最初に抗がん剤を使っていた患者は抗がん剤を使わねばならぬ理由があるから使っており、一方で抗がん剤を使っていなかった患者は抗がん剤を使う必要がないから使っていなかったわけです。

より具体的に言えば、抗がん剤を使っていた患者はそれだけ癌のステージが進行しており、抗がん剤を使っていなかった患者はそこまでステージが進行していなかったのでしょう。


つまり、元々の抗がん剤群の患者は癌のステージが４で、非抗がん剤のステージは１だったのです。

ですので、RCTで実現されていたように「治療あり・なしの２群間で交絡因子の分布が均質」にはなっていません。

となるとタイムマシンで時を戻して治療を入れ替えたとしても、抗がん剤群はステージ１の患者となり、非抗がん剤群はステージ４の患者となるので、最初の研究のように「抗がん剤群の１年後生存率は20%、非抗がん剤群のそれは50%」とはなりませんよね？

より専門用語で言い換えると、「癌のステージが交絡因子となり、Exchangeabilityが実現できていない状況」です。

Exchangeabilityを数式で表す

では、ここまで説明してきたExchangeabilityを数式で表してみましょう。

Pr[Y^{a=1}|A=1] = Pr[Y^{a=1}|A=0] = Pr[Y^{a=1}]

「いきなり暗号が出てきたぞ」と思う方は、こちらの記事の解説をご覧ください。
※Vol.2 二つの効果：個人因子効果と集団因子効果の違いとは

この式の意味を説明していきましょう。

Pr[Y^{a=1}|A=1]

まず、”|”は条件付けを表し、ここでは”「A=1」だった人たちにおいて”ということを意味します。つまり、実際に抗がん剤治療を受けた人たちにおいて、という意味です。

次に”Y^{a=1}”は、”A=1だった人たちが、仮にA=1となった時に、Y=1となる”ということを意味します。「何言ってるんだ」と思われたかもしれませんが、ただ単に「実際に抗がん剤治療を受けた人が（A=1）、生存した（Y=1）」という当たり前のことを言っているだけです。

最後にPrは確率を表しますので、つまり上の式は「実際に抗がん剤治療を受けた人が生存した確率」を表していることになります。

Pr[Y^{a=1}|A=0]

まず、”|”は条件付けを表し、ここでは”「A=0」だった人たちにおいて”ということを意味します。つまり、実際に抗がん剤治療を受けなかった人たちにおいて、という意味です。

次に”Y^{a=1}”は、”A=0だった人たちが、仮にA=1となった時に、Y=1となる”ということを意味します。つまり、抗がん剤治療を受けなかった人たちが、仮に治療を受けた際に生存する、ということですね。

最後にPrは確率を表しますので、つまり上の式は「実際に抗がん剤治療を受けなかった人が、仮に受けた時に生存した確率」を表していることになります。

Pr[Y^{a=1}|A=1]　= Pr[Y^{a=1}|A=0]

上記を踏まえると、この式の意味は「実際に抗がん剤治療を受けた人が生存した確率」と「実際に抗がん剤治療を受けなかった人が、仮に受けた時に生存した確率」が等しい、ということです。

つまり、「治療を受けた群と受けたなった群において、治療の有無を交換しても結果が変わらない」ということになりますので、これまで説明してきたExchangeabilityですね。

Pr[Y^{a=1}|A=1] = Pr[Y^{a=1}|A=0] = Pr[Y^{a=1}]

さて、とするとExchangeabilityが成立していれば「実際にどんな治療を受けたか」ということは仮想世界における治療効果を推定する上では不要な情報になるため、”|A=1”と”|A=0”は無視できる、ということになります。

それにより、左辺の式から”|”で表現される条件付けが削除され、最終的にPr[Y^{a=1}]となりました。

因果推論におけるExchangeabilityの意義

ここまででExchangeabilityのナラティブ及び数式での説明を行ってきました。

ではいよいよ、「なぜAssociationからCausationを推論するうえでExchangeabilityが大切なのか」ということを解説していきましょう。

これを考える上で、Exchangeabilityともう一つ、Consistencyという概念が登場しますが、その解説はまた別の記事にて後日公開予定ですのでお楽しみにしていてください。

リスク差を計算する時、Associationを数式で表すと

Pr[Y=1|A=1] ≠ Pr[Y=1|A=０]

Causationを数式で表すと

Pr[Y^{a=1}=1] ≠ Pr[Y^{a=0}=1]

でした。

※「ん？」と思った方はこちらの記事で初心者向けにわかりやすく解説しています。

ですので、「AssociationからCausationを推論する」には、上の式を下の式に変換できれば目的を達成できることになります。

では、実際に数式を使いながら考えていきましょう。

まず、Associationより

Pr[Y=1|A=1] - Pr[Y=1|A=０]

そして、Consistencyによって

Pr[Y^{a=1}] =  Pr[Y|A=a]

なので、これを上の式に適用すると

Pr[Y=1|A=1] - Pr[Y=1|A=0] = Pr[Y^{a=1}=1|A=1] - Pr[Y^{a=0}=1|A=0]

そしてExchangeabilityによって

Pr[Y^{a=1}|A=1] = Pr[Y^{a=1}|A=0] = Pr[Y^{a=1}]

なので、

Pr[Y^{a=1}=1|A=1] - Pr[Y^{a=0}=1|A=0] = Pr[Y^{a=1}=1] - Pr[Y^{a=0}=1]

これにより、Associationの式が、Causationに変換できました。

Randomizationの限界

なおRandomizationを行ったとしても、Exchangeabilityが必ずしも成立するとは限らないことに注意が必要です。

そのため「RCTをすれば必ず交絡因子の影響を除去できる」とは言わず、「適切なRCTをすれば理論的には交絡因子の影響を除去できる」と表現すべきです。


例えば、サンプルサイズが小さい場合には割り付けに偏りが生じ、交絡因子が両群でバランシングされない場合があります。

カジノでルーレットをしても、一時点を切り取れば「赤が連続して8回出る」といったことが起こる想像をしてください。


同じように、抗がん剤の有無をランダム割り付けしても、抗がん剤あり群に偶然ステージ３のがん患者が多く集まったということも確率的には起こり得ます。

こうした事態を防ぐために行われるのがConditional randomization（条件付けランダム化）です。

Conditional randomizationとは

Conditional randomizationの定義

Conditionalとは直訳すると”条件付き”という意味になります。

例えば抗がん剤治療の有無をランダムに割り付けることを考えましょう。

抗がん剤の有無が生存率に与える影響を調べる上で、両群で癌のステージをバランシングすることは極めて重要です。

なぜなら、片方の群にステージが重い癌患者が偏ってしまった場合、抗がん剤の影響がステージに交絡されてしまい、因果効果を頑健に求めることができなくなってしまうからです。


そこで登場するのがConditional randomizationです。

一体何を「条件づける」のかと言えば、そうです、癌のステージです。
対象集団全体を、ステージの大小で0/1の２群に分け、そしてそれぞれの群の中でランダムに治療を割り付けたとしましょう。

当然ながらそれぞれの群内ではステージが均質に揃えられていますので、「偶然ステージの分布が偏る」ということは発生し得ません。


つまりこれは、「ステージという条件付けの中で、Exchangeabilityが成立している」状況です。

そして、観察研究のデータで因果推論を行う際に実現しようとしているのがこのConditional Exchangeabilityです。


観察研究では当然ながらRandomizationは行われておりませんので、抗がん剤の曝露群・非曝露群でExchangeabilityが成立することはありません。


では、観察研究ではAssociationからCausationを推論することはできないのでしょうか？

いいえ、そうではありません。

上の例でステージでRandomizationを条件付けたように、観察研究においても両群においてバランシングせなばならない因子、つまり交絡因子が全て測定されていれば、その交絡因子で対象集団を条件づけることで、Exchangeabilityを実現することができます。

例えば、抗がん剤と生存率の因果関係を調べる上で、交絡因子がステージ、併存疾患、家族歴の三つしかなかったとしましょう。

議論を簡便にするためにそれぞれ0/1のカテゴリー変数とします。

この時、条件付けを行うと2×2×2で8つの患者集団が出来上がります。

あとはそれぞれの集団の中で曝露群・非曝露群を比較してやればExchangeabilityが担保されます。


このように、条件付けの上で達成されるExchangeabilityをConditional exchangeabilityと呼び、一方で条件付けなしで達成されるExchangeabilityをMarginal exchangeabilityと呼びます。

Conditional exchangeabilityを達成する上で大切なことが、「すべての交絡因子が適切に測定されている必要がある」ということです。

これが観察研究の大きなリミテーションの一つなのですが、すべての交絡因子が適切に測定されているためには以下の二つの条件が必要になります。

・その曝露・アウトカムの因果関係におけるすべての交絡因子が明らかになっている
・そしてそれらの交絡因子が正しく測定できている

例えば「喫煙と肺がん」の因果関係を調べる際、我々人類は「すべての交絡因子を明らかにしている」と言うことができるでしょうか？

いいえ、難しいでしょう。

肺がんの罹患において我々が知り得ていないメカニズムが存在し、そこに未知の交絡因子が存在するということは否定できません。


我々にできるのは「先行研究から明らかになっている交絡因子を精一杯測定し、その上で”未知の交絡因子の影響は大きくはない”という仮定をおいた上で結果の頑健性をクリティークする」ということのみです。

Conditional randomizationを数式で表す

このConditional exchangeabilityを数式で表すと、以下のようになります。

Pr[Y^a|A=1, L=1] = Pr[Y^a|A=0, L=1]

ご覧の通り、Exchangeabilityの式に"L=1"が追加されているのがわかりますね。

この式は、以下のようにも表現できます。

Y^a⫫A|L　　(Lで条件付けた際にAとYが独立)

まとめ

• Randomizationを行うことで集団の背景因子の分布を均質化することができる

• これによってExchangeabilityが達成され、AssociationからCausationを推論する条件の一つが達成できる

• 観察研究においては、すべての交絡因子が適切に測定されていればConditional exchangeabilityを達成することができる

参考文献

ウェブサイト

• 津川友介. 統計学における因果推論（ルービンの因果モデル）（https://healthpolicyhealthecon.com/2014/11/30/rubincausalmodel/）

参考文献

1. Murad MH, Asi N, Alsawas M, et al. New evidence pyramid. BMJ Evidence-Based Medicine. 21, 125-127 (2016).

参考図書：『Causal Inference: What If』

Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。

mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。

そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンズホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？-