
【疫学専門家監修】DAGを徹底解説 | 基礎編:因果推論の必須ツールで、交絡因子を可視化する - ゼロから学ぶ因果推論 vol.12-1
2025.04.22
シリーズ紹介|ゼロから学ぶ因果推論
「医学研究は難しい」、きっと多くの方がそう感じているでしょう。
因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。
因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。
「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。
はじめに
治療とその効果の因果関係を正しく捉えることは、一見すると簡単そうに思えるかもしれません。
しかし実際には、交絡やバイアスに気づかずに誤った結論へと導かれてしまうケースは少なくありません。
こうした“落とし穴”を回避して正確な因果推論を実践するための必須ツールがDAG(Directed Acyclic Graph)です。
DAGは、複雑な因果関係を直感的に図で表現できるツールであり、「どの変数を交絡因子として調整すべきか?」といった問いを明確に整理することができます。
この記事では、DAGをはじめて学ぶ方でも理解できるように前編(DAGの基礎編)と後編(DAGの応用編)に分け、DAGの基本的な考え方と魅力を具体例を交えながらわかりやすく解説します。
mMEDICI Library | ひらけ、叡智の扉
叡智の扉を、全ての人が開けるように——。
学びは、限られた豊かな人々だけの特権ではありません。
経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。
mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。
隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。
「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。
- シリーズ紹介|ゼロから学ぶ因果推論
- はじめに
- mMEDICI Library | ひらけ、叡智の扉
- この記事のまとめ
- この記事を読むと分かること
- この記事は誰に向けて書かれているか
- 因果推論シリーズ
- 執筆者の紹介
- 編集者
- 監修者
- 1.因果ダイアグラム(DAG)とは何か?
- DAG(Directed Acyclic Graph)の定義
- 2.DAGを構成する要素
- 3.DAGの基本的な読み方
- 4.なぜDAGが必要なのか
- 因果関係の視覚化・整理
- 因果関係の仮定の明確化
- DAGによって実現するコミュニケーション
- 5.DAGを使わない場合の問題点
- 6.DAGがもたらすメリット
- 1.交絡因子や他の要因を整理できる
- 2.因果推論の仮定を明確に提示できる
- 7.バックドアパスとは?
- バックドアパスの定義
- 「バックドアパス」とはどのような経路なのか?
- バックドアパスと交絡の関係
- バックドアパスの見つけ方
- バックドアパスの調整法
- 8.前編(基礎編)のまとめ
- 参考文献
- 因果推論を学ぶならオンラインスクールmJOHNSNOW
- 【YouTubeラジオコンテンツ 耳から学ぶシリーズ】
- シリーズ紹介|ゼロから学ぶ因果推論
この記事のまとめ
この記事を読むと分かること
因果ダイアグラム(DAG)とは何か
因果ダイアグラム(DAG)を使用する意義
バックドアパスと交絡について
この記事は誰に向けて書かれているか
因果推論を学び始めた初学者の方
因果ダイアグラム(DAG)の基本を知りたい方
DAGを読み解けるようになりたい方
因果推論シリーズ
vol.1:因果推論の出発点 - 因果と関連の違いとは? -
vol.2:因果効果の基本を徹底解説 - Individual Causal Effect(個人因果効果)とAverage Causal Effect(平均因果効果)の違いとは? -
vol.3:初心者のためのTarget Trial Emulation(TTE)
- Part 1 ; ETAFOCAフレームワークについて
- Part 2 ; 三つの時点で考えるバイアスとその対処法
- Part 3 ; 論文の実例で理解を深めるTTEvol.4:Exchangeability(交換可能性)を徹底解説 - Randomization(ランダム化)が実現する因果推論の必須条件 -
vol.5:Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.6:Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.7:Consistency(一致性)を徹底解説 - 観測データと反事実アウトカムを一致させよ -
vol.8:Positivity(正値性)を徹底解説 - 因果推論の落とし穴を回避せよ -
vol.9:Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
vol.10:効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか? -
vol.11:交互作用を徹底解説 - 複数の介入による相乗効果 -
vol.12:DAGを徹底解説
vol.13:交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
vol.14:選択バイアスを徹底解説 - 消えた患者が結果を歪める?-
執筆者の紹介
氏名:松下翔
所属:橋本市民病院総合内科
自己紹介:東京大学医学部を卒業後、天理よろづ相談所病院で初期研修・後期研修(内科ローテートプログラム)を行い、内科専門医を取得。その後、京都大学公衆衛生大学院 医療疫学教室博士後期課程に進学。現在は橋本市民病院総合内科フェローとして常勤で臨床を続けながら、社会人大学院生として疫学を学んでいる。
編集者
氏名:菊池祐介
所属:mMEDICI株式会社
専門性:作業療法学修士。首都大学東京(現東京都立大学)・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。
監修者
氏名:廣瀬直紀
所属:mMEDICI株式会社
専門性:保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。
1.因果ダイアグラム(DAG)とは何か?
DAG(Directed Acyclic Graph)の定義
因果ダイアグラム(DAG: Directed Acyclic Graph)は、複雑な因果関係を視覚的に整理し、因果推論を支援するツールです。
(因果関係を整理する際には、特に”causal DAG” と呼ばれることもあります。)
DAGを直訳すると有向非巡回グラフと呼びます。
その名の通り「有向である(Directed)」ということと「巡回しない(Acyclic)」という二つの性質を持つグラフをDAGと言います。
「有向」も「非巡回」も聞きなじみがないので、「なんのこっちゃ?」と思われるかもしれません。
簡単にいうと「原因」と「結果」を矢印で結んだ図です。
とてもシンプルですよね?
ここからは「有向」と「非巡回」が意味するところを具体的に説明していきます。
有向(Directed)とは?
「因果関係を矢印(→)がついた線で表現する」こと
例えば、XがYの原因である場合、X → Yと記述します。

通常、Y ← X と書くことはなく、 X → Yのように左から右に向かう向きに記述します。
左から右に書くことで、時系列の流れとなり理解しやすくなります。
非巡回(Acyclic)とは?
「矢印をたどってもループが発生せず、時間的順序が守られる」こと
因果関係は時間的概念を含むので、XがYを引き起こす場合、Xが先に起きていなければなりません。
つまり、YがXを引き起こすことはありません。
Xが巡り巡ってX自身を引き起こすということはあり得ないためです。
ゆえに、グラフが巡り巡って元に戻ることはありません。
具体例を示すと、下図のように巡回しているグラフはDAGと呼びません。

2.DAGを構成する要素
ノード(変数)とエッジ(因果関係をあらわす矢印)の組み合わせでDAGが構成されます。
ノード(変数)
関心のある因果関係に関わる確率変数のことをノード (変数)と呼びます。
確率変数には関心のある曝露とアウトカムの他に、交絡因子、コライダー、媒介変数などが含まれます。これらの変数については本記事の後半と、応用編で詳しく解説します。
図1のX → YというDAGにおいて、X(曝露)とY(アウトカム)がノードにあたります。
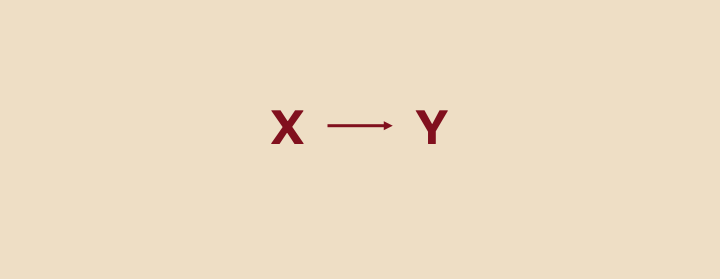
エッジ(因果関係を示す矢印)
あるノードXが別のノードYを引き起こす因果関係がある場合、「X → Y」のようにエッジ(因果関係を示す矢印のこと)を書きます。
逆に、二つのノードの間にエッジ(矢印)がないことは、両者の間に因果関係がないことを示しています。
X(曝露)とY(アウトカム)の間の因果関係に関心がある場合、X → Yという両者の関係を主眼に考えますが、XとYの双方に影響を与えるノード(変数)が実際にはたくさん考えられます。
それらを臨床的な知識(ドメイン知識)をもとに検討し、研究を計画する段階でDAGを記載していきます。
3.DAGの基本的な読み方
DAGの読み方はとても直感的です。
基本的には、矢印(→)を追いかけるだけです。
具体例をもとにして考えていきましょう。
「喫煙が肺癌の原因か?」というリサーチクエスチョンを想定した時のことを考えます。
関心のある曝露は「喫煙」であり、アウトカムは「肺癌」です。
これをDAGで記載するとどのように書けるでしょうか?

上記のDAGにおいて、喫煙と肺癌がノード(変数)で、その間にエッジ(因果関係を示す矢印)が書かれています。
喫煙が原因で肺癌が起きているという因果関係を示しています。
つまり、もし喫煙と肺癌に影響を与えるような他の重要な変数が存在しないと仮定できるなら、「喫煙者は肺癌になりやすい」という関連がみられた時に、単なる偶然や交絡ではなく、実際に喫煙が肺癌を引き起こしていることを示していると言えます。
このように、隣接する矢印は直接的な因果効果を示します。
4.なぜDAGが必要なのか
因果関係の視覚化・整理
DAGを用いることで、因果関係を視覚的に整理することができます。
これは非常に直感的で理解しやすいという点が大きな強みです。
特に「どの共変量を調整すべきか」を判断する際に、DAGは有効なツールとして力を発揮します。
不要な調整を避け、最小限の交絡因子を適切に調整する助けになります。
因果関係の仮定の明確化
DAGを用いることで、因果関係に関する仮定を明確にすることができます。
ほとんどの疫学研究は、さまざまな仮定のもとにデザインされていますが、これらの仮定が明示されていないことが少なくありません。
DAGを描くことで、研究に内在する因果関係の前提を視覚的かつ体系的に表現することが可能となります。
例えば、詳細は後述しますが、交絡因子など多様な変数の関係性をDAGを用いて整理することで、因果関係の仮定を明確にすることができるのです。
DAGによって実現するコミュニケーション
DAGを用いて因果関係を図でわかりやすく整理することで、研究者の間でコミュニケーションがとりやすくなります。
例えば自分が消化器内科医だったとして、生活習慣と大腸癌の因果関係を調べる研究を実施したい時、生活習慣と大腸癌の双方に関わる交絡因子が何か、同じ消化器内科医にはわざわざ図を書かなくても伝わるかもしれません。
それは、同じ専門性をもつ医師同士であれば、暗黙の了解として背景にある臨床の知識(ドメイン知識)を共有しているからです。
しかし、特に臨床研究においては、専門性が異なる複数の職種の方と共同で研究を実施することも多いと思います。疾患について専門でない統計家の先生に解析についてコンサルテーションすることもあるでしょう。
その際に、どのような因果関係の仮定をおいているのか、DAGを用いれば明瞭に同じ土俵の上で考えることができます。
研究者間のコミュニケーションを円滑にし、意思決定を行うためにDAGは必要不可欠です。
5.DAGを使わない場合の問題点
DAGを使わずに文章だけで研究の仮説や因果関係を考えた場合、重要な交絡因子を見落としてしまったり、因果の構造を誤って解釈してしまうリスクが高まります。
交絡とは、共通の原因によって引き起こされるバイアスのことです。また、交絡因子は曝露とアウトカムの関連に影響を与える「共通の原因」のことです。
とあるリサーチクエスチョンの例を題材にして、DAGを使わずに文章だけで曝露・アウトカム・交絡因子の関係性を表現してみましょう。
リサーチクエスチョン:「疾患A」に対する「新薬」が「死亡率」を低下させるか?
「新薬を飲んだグループ」と「新薬を飲まなかったグループ」とで両者の死亡率を比較することにしました。
研究者は当然「新薬を飲んだグループ」の方が死亡率が低くなることを期待します。
ところが「新薬を飲んだグループ」の方が死亡率が高いことが分かりました。
その理由は「疾患Aの重症度」が高い人に対して積極的に新薬が処方されていたからです。
つまり「疾患Aの重症度」が高い人は死亡リスクも高く、結果的に「新薬の飲んだグループ」は「死亡率が高い」という見かけ上の関係が生じたのです。
すなわち「疾患Aの重症度」が新薬と死亡の関係における交絡因子となっていたのです。
この説明を読みながら、きっと皆さんは「重症度が新薬と死亡率に影響していて、新薬は死亡率を…」と、それぞれの関係性を頭の中で思い描いていたはずです。
もしも交絡因子が三つ、四つと増えた場合を想像すると、それらの関係性を文章で表現し、クリアにイメージすることは至難の業です。その結果、重要な交絡因子を見落としたり、因果の構造を誤って理解してしまうことは容易に想像できますね。

DAGを記載するとそれぞれの関係性が一目瞭然ですね。
「新薬→死亡」という興味のある因果関係に影響を与える変数として、「重症度」という変数が記載されています。
「重症度が高い」と新薬が処方されやすいため、重症度→新薬という関係があります。また、「重症度が高い」人は「死亡率が高い」ため、重症度→死亡という矢印が伸びています。
つまり「重症度」は、新薬の使用と死亡の両方に影響を与える共通の原因(common cause)です。
このように、新薬と死亡との関係において、重症度が交絡因子として働いていることを、DAGを用いて視覚的に表現することができます。
DAGを描くことで、因果構造が一目で分かりやすくなり、重症度が交絡因子であることを直感的に理解することが可能になります。
DAGを使わなかった場合の問題点と、DAGを使うことの意義がご理解いただけたでしょうか?
6.DAGがもたらすメリット
1.交絡因子や他の要因を整理できる
DAGを記載することで、以下のような因果推論における重要な要素を視覚的に整理できます。
①交絡因子(共通の原因)
②コライダー(共通の結果)
③媒介変数(暴露とアウトカムの間の中間因子)
それぞれの概念とDAGによる表現について簡単にご説明します。(詳細は後編(応用編)で解説します。)
①交絡因子
「交絡」とは「共通の原因」によって起こるバイアスのことで、交絡を引き起こす変数を「交絡因子」と呼びます。
DAGで記載するとCが「交絡因子」に該当します。

先ほどの例「新薬(X)」 と「死亡率(Y)」 の関係における「重症度(C)」が交絡因子の例に当たります。
②コライダー
「コライダー」とは、曝露とアウトカムの「共通の効果」となる変数のことを指します。
DAGで表すとSがコライダーに該当します。
たとえば、「学力(X)」 と「運動能力(Y)」 の関係を考えるとします。
学力が高いと入学試験に合格しやすく、運動能力が高くても合格しやすい場合、「合格者 (S)」は学力と運動能力の両方の影響を受ける「共通の効果」となり、Sはコライダーとなります。

③媒介変数
「媒介変数」とは、曝露とアウトカムの間にある中間因子のことです。DAGで記載するとMが媒介変数に該当します。

たとえば、「運動」することで「血圧」が下がり「心疾患疾患リスク」が下がるというメカニズムが考えられる時、「運動(X)」 と「心疾患疾患リスク(Y)」の因果関係において、「血圧(M)」が媒介変数 となっています。
「コライダー」「媒介変数」については後編(応用編)で詳しく解説します。
2.因果推論の仮定を明確に提示できる
臨床研究で因果推論を行うためには、どの変数を交絡因子と捉え、またどの変数が媒介変数なのか、、、といった様々な仮定が必要です。
しかし多くの場合、これらの仮定が明示されていないことが多く、因果推論の根拠がブラックボックス化してしまうのです。
DAGを記載することで、研究における因果推論の仮定を明確に提示することができます。
具体例:「運動」と「健康」の関係
「運動している人は健康である」という観察研究のデータがあるとします。

DAGを用いない場合
単純な統計分析を行うと、運動と健康の間に「関連(association)」があることがわかったとします。しかし、なぜその関連があるのかが不明なまま「運動は健康に良い」と短絡的に解釈してしまう可能性があります。
DAGがある場合
DAGを用いることで「運動」と「健康」の関係に影響を与える可能性のある要因(交絡因子や媒介変数)を可視化することができます。

例えば「若い人のほうが運動して、若い人のほうが健康状態がよい」場合、「年齢」が運動と健康の関係の交絡因子となります。
また「運動」することで「血圧」が低下し「健康」になる場合、「血圧」が「運動」と「健康」の媒介変数となります。
このようにDAGを描くことで、交絡因子や媒介変数といった因果推論の仮定をクリアに整理し、視覚的に明示できるようになります。
7.バックドアパスとは?
バックドアパス(backdoor path)は因果推論における重要概念のひとつで、交絡の有無を判断し、調整すべき変数を見極めるための基本的な考え方です。
バックドアパスの定義
バックドアパスとは「曝露に向かって」矢印が伸びる経路であり、交絡を生じさせる経路として重要な意味をもちます。
日本語では「裏口経路」と呼ばれることがあります。いわば、因果効果の推定を歪める「裏ルート」です。
バックドアパスを理解するためには、DAGにおけるパス(経路)の種類や矢印の方向づけのルールを知る必要がありますので、ひとつひとつ理解していきましょう。
「バックドアパス」とはどのような経路なのか?
まず「バックドアパス」を理解する前に「有向経路」と「非有向経路」について整理しておきましょう。
「有向経路」と「非有向経路」はDAGの矢印の向きによって分類されます。
以下のDAGは有向経路と非有向経路を色分けしたものです。

有向経路
曝露からアウトカムに向かって、矢印の向きが一貫して同じ方向に進んでいる経路のことを指します。
上の図においてはX → YやX → M → Yが有向経路です。
曝露(X)からアウトカム(Y)に向かって同じ方向に矢印が伸びていますね。
非有向経路
曝露からアウトカムに至る経路の中で、矢印の向きが途中で逆転するような経路のことを指します。
上の図においてはX ← C → YやX → S ← Yが非有向経路です。
曝露(X)からアウトカム(Y)に向かって矢印をたどろうとした時、逆向きの矢印(X ← C、S ← Y)が途中でみられますね。
バックドアパスは、非有向経路の一つと言えます。
以下の二つの図は、バックドアパスをDAGで示したものです。


どちらもXからYに直接向かう矢印がありませんので、XとYの間に因果関係はありません。
しかし、X ← C → Y、X ← C → D → Yのように「裏口」を通してXからYまでの経路がつながっています。
この場合、実際にはXとYの間に見かけ上の関連が生じてしまうことになります。このような状態のことを「バックドアパスが開いている」と表現します。
バックドアパスと交絡の関係
ここからは「なぜバックドアパスによって交絡が生じるのか」について解説していきます。
具体例として、先ほど紹介した「新薬(X)」「死亡率(Y)」「重症度(C)」の関係を示したDAGを用いて考えてみましょう。
このDAGでは「重症度(C)」が「新薬(X)」にも「死亡率(Y)」にも影響しており、X ← C → Y というバックドアパスが成立しています。
つまり「新薬(X)」と「死亡率(Y)」の間に、交絡因子「重症度(C)」を通じたバックドアパスが開いている状態です。
「重症度」が高い人ほど「新薬」を処方されやすく、かつ「死亡率」が高いため「新薬を使った人の方が死亡率が高い」という見かけの関連が観察されてしまう可能性があります。
これがまさに「新薬」による「死亡リスク」に対する因果効果の推定が、交絡因子「重症度」を通じたバックドアパスによって歪められている状態です。
バックドアパスの見つけ方
バックドアパスの見つけ方は簡単です。
① 最初に、関心のある曝露とアウトカムを同定します。
② 次に、曝露に向かって入る矢印を同定します。
③ その経路がアウトカムYに向かっている時、バックドアパスは開いています。
バックドアパスの調整法
バックドアパスを「閉じる」ためには、バックドアパスを通る変数を少なくとも一つ調整する必要があります。
ある変数を同じ条件のもとで条件付けた場合、その変数を□で囲みます。
□で囲まれた変数のところでバックドアパスを閉じることができます。
例えば以下の図では、X ← C → Yの経路ではCで条件付けるとバックドアパスを閉じることができます。

また、以下の図では、X ← C → D → Yの経路ではCまたはDのいずれかを条件付けるとバックドアパスを閉じることができます。

CとDの両方を調整する必要はなく、バックドアを閉じるために最小限の共変量としてCまたはDの調整を検討すればよいと分かります。
すなわち、たとえ変数Cが測定できていなくても、変数Dが測定できていれば、Dで調整すれば大丈夫です。
このように、DAGを書くことで調整すべき最小限の共変量のセットを考えることができます。
調整の方法は下記のようなものがあります。
① 層別化(例えば年齢ごとに分けて分析する)
Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
② 逆確率重み付け (同じ条件の擬似集団を作る)
Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
③ マッチング(同じ条件の人同士を比較する)
④ 回帰分析で変数をモデルに入れる
このように、最小限の共変量のセットで調整を行うことで、交換可能性を担保することができます。
具体例として「運動が心疾患リスクを低下させるか?」という疑問に対するDAGを考えてみましょう。
曝露である運動が、アウトカムである心血管リスクに与える影響をみたいため、まず「運動→心疾患リスク低下」という関係を書きます。
しかし「若年者」ほど「運動」しやすく、「若年者」ほど「心血管リスク」が低いことを考慮しないといけません。「年齢」が「運動」と「心血管リスク」の共通の原因となっています。

この時「同じ年齢」の人を対象として「運動」と「心血管リスク」の関係を調べる方法(層別化)などによって「年齢」を調整することができます。
ある変数を同じ条件のもとで条件付けた場合、その変数を□で囲みます。
□で囲まれた変数のところでバックドアパスはブロックされ、「年齢」が「運動」や「心血管リスク」に与える影響を無視することができます。
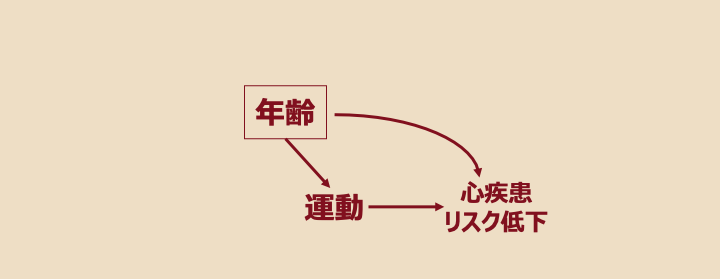
例えば層別化では「同じ年齢」の人どうしで比べているので、当然ですよね。
このように「年齢」で条件付けることで「運動」と「心血管リスク」低下の因果効果の推定を歪める年齢という交絡因子の問題に対処できています。
「バックドアパスは、交絡因子で条件付けるとブロックされる。」
(四角い囲みが壁となって裏口経路が通れなくなるイメージです)
このルールはとても重要ですのでぜひ覚えておきましょう。
8.前編(基礎編)のまとめ
ここまで、DAGの定義や構成要素(ノードとエッジ)、基本的な読み方に加えて、バックドアパスと交絡因子の基本的な考え方についても学びました。
後編(応用編)では、DAGをより応用的に活用し、因果推論において重要な変数である「コライダー」や「媒介変数」などの概念を深掘りしていきます。より
応用的な知識を深めていきましょう!
参考文献
井上浩輔.医学研究のための因果推論レクチャー.医学書院2024
鈴木越治.医学における因果推論 第5部.日本衛生学雑誌2009年64巻4号p. 796-805.doi:https://doi.org/10.1265/jjh.64.796
Digitale JC, Martin JN, Glymour MM. Tutorial on directed acyclic graphs. J Clin Epidemiol. 2022;142:264-267. doi:10.1016/j.jclinepi.2021.08.001
Lipsky AM, Greenland S. Causal Directed Acyclic Graphs. JAMA. 2022;327(11):1083-1084. doi:10.1001/jama.2022.1816
Feeney T, Hartwig FP, Davies NM. How to use directed acyclic graphs: guide for clinical researchers. BMJ. 2025;388:e078226. doi:10.1136/bmj-2023-078226
"矢印"をつかって因果関係を視覚的に整理する:因果ダイアグラム(DAG)入門①〜なぜDAGが必要なのか〜https://www.krsk-phs.com/entry/DAG1
参考図書:『Causal Inference: What If』
Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。
mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。
因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。
そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。
mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。
本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです!
・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ(ex. RWDピア)
・24時間利用可能なオンライン自習室「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください!
・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催【YouTubeラジオコンテンツ 耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。
すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。
シリーズ一覧
シリーズ紹介|ゼロから学ぶ因果推論
「医学研究は難しい」、きっと多くの方がそう感じているでしょう。
因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。
因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。
「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。
因果推論シリーズ
vol.1:因果推論の出発点 - 因果と関連の違いとは? -
vol.2:因果効果の基本を徹底解説 - Individual Causal Effect(個人因果効果)とAverage Causal Effect(平均因果効果)の違いとは? -
vol.3:初心者のためのTarget Trial Emulation(TTE)
- Part 1 ; ETAFOCAフレームワークについて
- Part 2 ; 三つの時点で考えるバイアスとその対処法
- Part 3 ; 論文の実例で理解を深めるTTEvol.4:Exchangeability(交換可能性)を徹底解説 - Randomization(ランダム化)が実現する因果推論の必須条件 -
vol.5:Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.6:Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.7:Consistency(一致性)を徹底解説 - 観測データと反事実アウトカムを一致させよ -
vol.8:Positivity(正値性)を徹底解説 - 因果推論の落とし穴を回避せよ -
vol.9:Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
vol.10:効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか? -
vol.11:交互作用を徹底解説 - 複数の介入による相乗効果 -
vol.12:DAGを徹底解説
vol.13:交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
vol.14:選択バイアスを徹底解説 - 消えた患者が結果を歪める?-
©mMEDICI Inc. ALL RIGHTS RESERVED.




















