【疫学専門家監修】Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ - ゼロから学ぶ因果推論 vol.8

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに

mMEDICI Libraryでは、これまでに「因果推論の識別３条件」のExchangeabilityとConsistencyについて解説してきました。

この記事では、３つ目の識別条件「Positivity（正値性）」について解説します。

Positivityを大まかに説明すると

「因果効果を推定するためのデータがきちんと存在している（＝正の値である）」

ことです。

Exchangeability、Consistencyと比べると、Positivityは「言うまでもなく、当然なこと」と思えますよね？

ところが、観察データに基づき因果推論を実践する上では絶対に見落とせないとても重要な概念です。

この記事では、Positivityの定義を踏まえた上で、Positivityが違反されるケースや対処方法について解説していきます。

最後までお読みいただいた後には因果推論において「Positivity」を考慮することの大切さがよく理解できることと思いますので、一つ一つ読み進めてみましょう。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• Positivityとは何か？

• Positivity違反の種類について

• Positivity違反の検出方法とその対処

この記事は誰に向けて書かれているか

• 因果推論を学び始めた初学者の方

• 因果推論の識別３条件を学びたい方

• Positivityの詳しい解説を読みたい方

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

執筆者の紹介

氏名：岡部 陽介
所属：理学療法士養成校 専任教員
経歴：理学療法士として５年間の臨床経験を経て、現在は理学療法士養成校で教員として勤務。ヘルスコミュニケーション、医療者と患者の共有意思決定（SDM：Shared Decision making）に関心を持つ。国際医療福祉大学大学院 医学研究科 公衆衛生学専攻。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。

1．Positivityとは

Positivity（正値性）を「どの条件をもつ個人においても、ある処置を受ける確率がゼロでない」ことを指します。

いきなりこの定義を聞いてもピンときませんよね？

まずは簡単なイメージを用いてPositivityについて考えてみましょう。

例えば、ある疾病に対する新薬があるとします。
臨床試験で「新薬を飲む人100名」と「新薬を飲まない人100名」とを比較することで、その疾病に対する薬の効果を調べることができます。

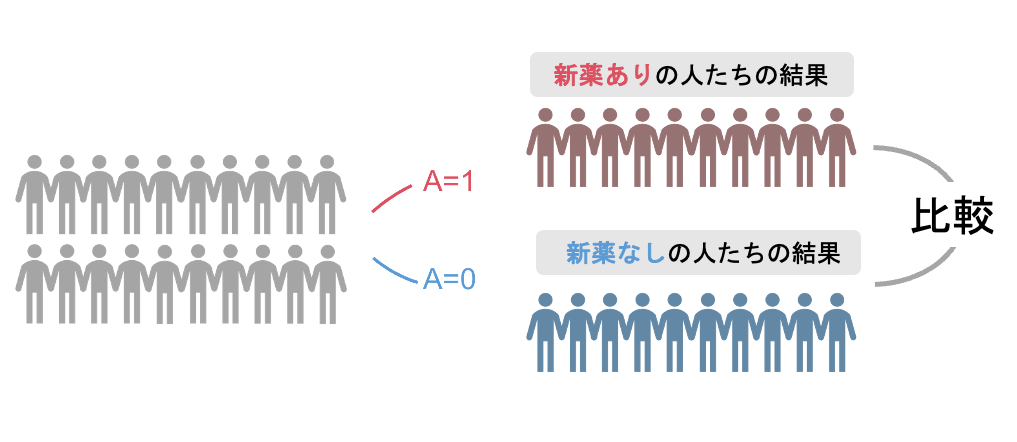
このように「新薬を飲む人」も「新薬を飲まない人」もきちんと存在していることが、Positivityが保たれた状況です。

この臨床試験の例を因果推論の考え方に発展させてみましょう。

まずは少し因果推論の考え方をおさらいします。

現実で得られる「実際に薬を飲んだ人たちの結果」から「もし全員が薬を飲んだ場合の結果」を推定します。

同じように、現実で得られる「薬を飲まない人たちの結果」から「もし全員が薬を飲まなかった場合の結果」を推定します。

このようにして「全員が薬を飲んだ場合の結果」と「全員が薬を飲まなかった場合の結果」の差を求めて因果効果を推論しました。

ここで、下のイラストのように「新薬を飲む人たちが0人」の場合、つまり「Positivityが違反された状況」を考えてみましょう。

そもそも「実際に薬を飲んだ人たちの結果」が存在しなければ、「もし全員が薬を飲んだ場合の結果」を推定することはできません。

このように、Positivityが因果推論を行う、そもそもの大前提であるということはよくお分かりいただけたことと思います。

ところで、皆さんもお気づきの通り、厳格な計画に基づいて実施される臨床試験において、「蓋を開けてみたら、コントロール群が一人もいない!!」などという状況は考えられませんよね。

Positivityを保証することなど自明なことですし、わざわざ考慮するまでもないように思えます。

「因果推論の識別３条件」のExchangeabiltyやCosistencyは「因果推論の根幹をなす仮定」という味わい深さがある一方で、Positivityは「そんなの当たり前」な印象があります。
（それ故にPositivityについて詳しく解説した記事にはなかなかお目にかかれないように思います。）

さて、このようにどこか掴みどころのないPositivityですが、観察研究においてはしっかりと念頭におかねばならないとても重要な条件です。

なぜなら「観察研究においてはPositivityが保証されない状況が十分に起こり得る」からです。


次の章からは、より詳しくPositivityの定義について考え、Positivityが違反されるケースやその対処法について解説していきます。

2．Positivityの定義と違反の種類

Positivityの定義は「どの条件をもつ個人においても、ある処置を受ける確率がゼロでない」ことでした。

「ある条件をもつ人たちが、ある治療を受ける確率がゼロ」になってしまう時を、Positivity violations（Positivity違反）と呼びます。

この記事ではPositivity violationsをStructural violations（構造的違反）とRandom violations（確率的違反）に分けて解説していきます。

2-1．Structural violation（構造的違反）

具体例を用いて考えてみましょう。
例えば観察データを用いて「新しい降圧薬（A=1）が高血圧患者に与える影響（Y）」について研究したいとします。

ここで、「妊娠している」という条件は「血圧」に強く影響するため、交絡因子として対処したいと考えたとしましょう。

ところが、この降圧薬は胎児への影響が不明なため、そもそも妊婦さんには投与されていない（A=1の確率が0%）ことがわかりました。

この場合には、「妊娠中の女性」は「新しい降圧薬」という治療を受ける可能性がゼロとなり、ここにStructural violationsが生じることとなります。

例えば、妊娠の有無を交絡因子としてIPW（逆確率重み付け）を行った場合は次のようになります。

「妊娠中」という条件においてStructural violationsが生じている時、分母がゼロになってしまいますので、IPWによって「もし妊娠中の女性が降圧薬を服薬した時」の結果を推定することはできません。


このように、Structural violationsがある場合は、「妊娠中の女性における新薬の効果」を計算によって補うことは難しく、最初から「妊娠中の女性を研究の対象外にする」といった対処をとる必要があります。

~Positivityの定義と交絡因子~

Positivityは「どの条件をもつ個人においても、治療を受ける可能性がゼロではないこと」と定義されます。この定義に基づくと、あらゆる交絡因子においてPositivityを要求するかのように思えますね。しかし、例で挙げたように「妊娠中の女性」に対する降圧剤処方が不可能で、Structural violationsが生じている場合にPositivityを保証することはできません。

因果推論の専門書「causal inference What if」ではPositivityの定義に対して次のように言及しています。

Actually,  this definition of positivity is incomplete because, if our study population were restricted to the group L = 1, then there would be no need to require positivity.

意訳すると「研究の対象が、ある条件を持つ（L=1）のグループに限定されていれば、L=0のグループにおいてはPositivityは必要ない」ということです。

つまり、Structural violationsが生じる場合に、研究の対象を限定することでPositivityの問題に対処することができると考えることができますね。

また、「どの条件をもつ個人においても…」とはいえ、「治療や結果に影響しない因子」（成書の中では”瞳の色が青い人”が例示されています）についてはPositivityを考慮する必要がないとも述べられています。「治療や結果に影響しない因子」であるかどうかを考えることは、すなわち交絡因子について吟味することに繋がりますね。

ここでは交絡因子について深掘りしませんが、「Positivity」と「交絡因子」は切り離すことができない概念ということになります。

2-2．Random violations（ランダム違反）

Random violationsは、Structural violationsのように治療の絶対禁忌があるわけではない（理論上、治療を受ける確率がゼロではない）場合に起こりうるPositivity違反です。

例えば、調整すべき交絡因子の数が増えるにつれてカテゴリの層が増えた場合に、Random violationsが起こりやすくなります。

分かりやすくイラストを用いて説明しましょう。

下のイラストは、ある治療における２つの交絡因子に対して層別化した時を表しています。

この場合、2×2×2＝8 つの層に分かれることになりますね。

もし、100名の対象者が８つの層に均等に分かれた時、１つの層に13名程度が存在することになります。

もちろん、実際には偏りが生じて人数が均等に分かれない場合もあるでしょう。

下のイラストのように、偶然にして０名の層が生じてしまうこともあるはずです。

これが、Random violationsです。

Random violationsは確率的に偶然に生じるPositivity違反と言えます。

ですので、サンプルサイズが大きくなればRandom violationsが解消される可能性が高まりますし、また異なるデータベースを用いた場合には先ほどとは別の層にRandom violationsが生じる可能性があります。

あり・なしの二値変数で表せる交絡因子が10個ある場合、治療Aの割り付けも掛け合わせると、なんと2,048個の層ができることになります。

この場合、たとえ10,000人のデータがあって全ての層に均等に分かれたとしても、各層には4〜5名しかいないことになります。調整すべき交絡因子の数が増えるほど、Random violationsが起こる可能性が高まることは容易に想像できるでしょう。

ひとまず、ここまでの説明でPositivity違反はStructural violations（構造的違反）とRandom violations（確率的違反）に分けて考えることができ、それぞれの特性についてご理解いただけたのではないでしょうか？

次の章からは、どのようにPositivity violationsを見つけ、どのように対処するのか考えていきましょう。

3．Positivity violationsの確認方法

ここまでの説明で、観察研究ではPositivity violationsが起こる可能性が十分にあることが分かりました。したがって、Positivity violationsが起きているのかをしっかりと確かめることが大切です。

この章では、実際にPositivity violationsが起こっているか確かめる方法として、Propensity Score（傾向スコア）を用いた方法を紹介します。

まずは傾向スコアについて簡単に確認しましょう。

傾向スコアは「その人がある治療を受ける確率」を表した指標と言えます。

特定の統計モデルを使うことで、複数の交絡因子を組み合わせて「このような交絡因子の組み合わせを持つ人は、このくらい治療を受けやすい傾向にある」という傾向スコアを算出することができます。

傾向スコアは0〜1.0の範囲の値を取り、0に近いほど「治療を受けにくい」、1.0に近いほど「治療を受けやすい」という性質を表しています。

突然、「傾向スコア」などという用語が登場して戸惑った方も多いことでしょう。

mMEDICI Libraryの過去記事の中で傾向スコアについて簡単に解説していますので、ぜひご覧ください。

交絡を調整せよ！ 逆確率重み付けを徹底解説 - ゼロから学ぶ因果推論 vol.6

傾向スコアの素晴らしい点は、複数の交絡因子の影響を「治療を受ける確率」という一つの指標に集約できることにあります。

例えば、調整すべき交絡因子が10個ある場合、層別化・標準化では全ての組み合わせで1,024個もの層に分かれることになりますが、傾向スコアを用いることで任意のスコア幅で層別化することができ、下のイラストのように10個の層に集約することが可能になります。

それでは、傾向スコアとPositivityのお話を結びつけて考えてみましょう。

例えば、年齢、性別、基礎疾患という３つの交絡因子があるとします。

計算により年齢：高齢、性別：男性、基礎疾患：ありという交絡因子を持つ人は傾向スコアが0.75ということがわかりました。つまり「治療を受ける確率が75%と推定される」ということになります。

例えば「傾向スコアが1.0」であれば、理論上「治療を受ける確率が100%」と考えられます。

つまり、仮に「傾向スコア1.0の人たち」が100名いたとすれば、「100名全員が治療を受ける」ことになります。言い換えると「傾向スコアが1.0の人たちは、治療を受けない確率がゼロ」と考えることができますね。

このように、極端な傾向スコアの値を持つ人たちが研究対象に含まれていた場合、Random violationsが生じる懸念が高まります。

ここで、傾向スコアをもとに、治療ありの人たちと治療なしの人たちの分布を、ヒストグラムで確認してみましょう。

このグラフをみると、傾向スコアの値が０や１に近い範囲において、治療群と非治療群のどちらか一方で「人数がゼロ」の層が生じていることが一目瞭然ですね。

・傾向スコア0.2以下の範囲で「治療あり」の人がいない
・傾向スコア0.8以上の範囲で「治療なし」の人がいない

このように、傾向スコアを用いることでPositivity violationsの状況を確かめることができました。

Positivityに類似した概念に Overlapというものがあります。

傾向スコアで治療群と非治療群の分布の重なり（overlap）を確認することでpositivity violationsの存在を確かめることができますね。

それでは、次の章でPositivity violationsに対する対処方について確認しましょう。

4．Positivity violationsがある場合の対処法

Positivity violationsが生じている場合はどうすればよいのでしょうか？

スタンダードな方法論が確立されている訳ではありませんが、Positivity violationsに対処する方法をいくつか紹介します。

4-1．トリミング（Trimming）

Positivity violationsのある部分を除外する方法です。

傾向スコアに基づいたトリミングでは、以下のようになります。

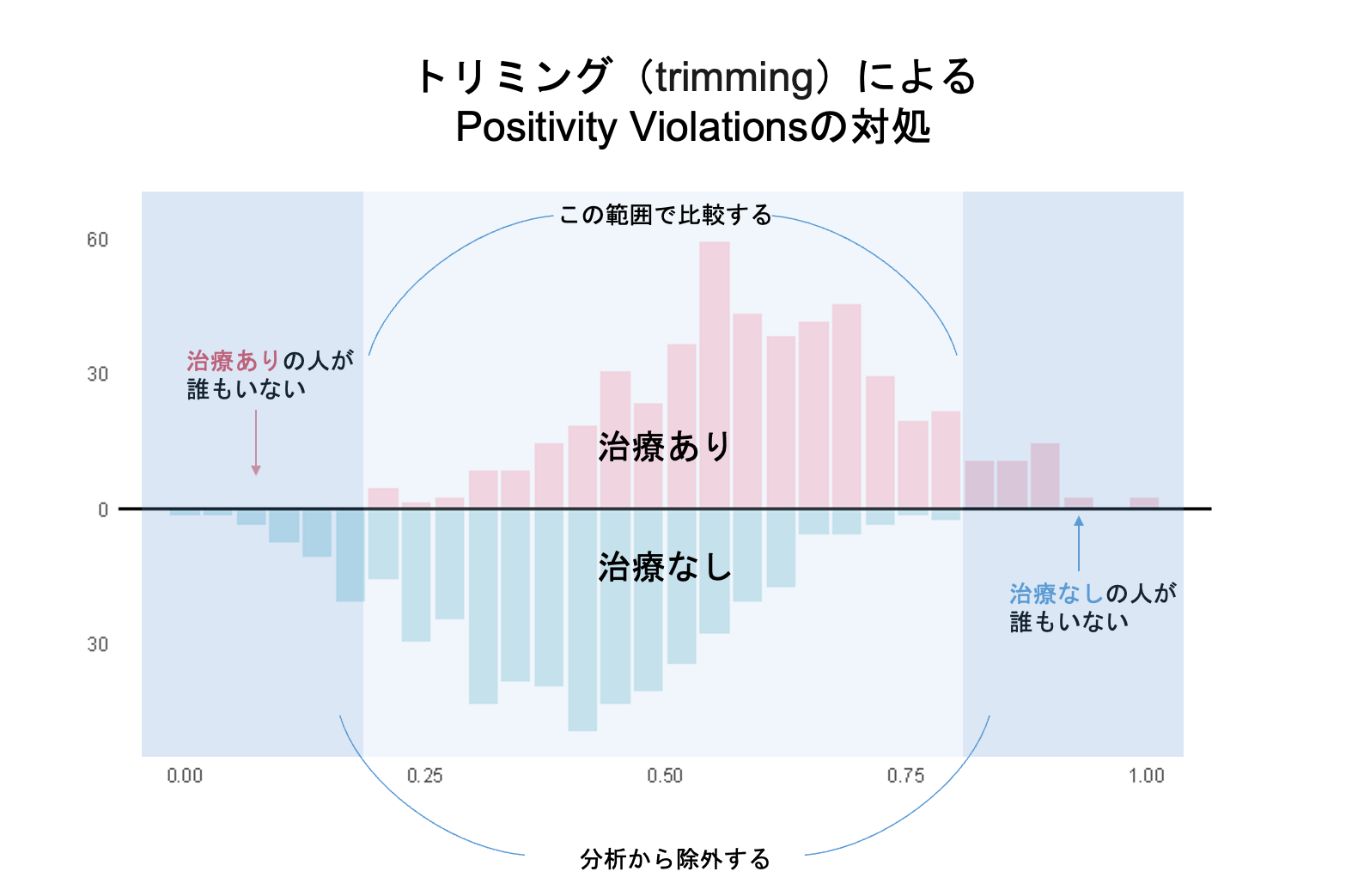
ただし、被験者を除外すると有効なサンプルサイズが減少してしまい、分析の精度が下がってしまう可能性があります。

また、特定の交絡因子の組み合わせをもつ人たちが分析から除外されることで、因果推論の対象が「〇〇以外の人たち」という特定のグループに限定されることにも注意が必要です。

4-2．外挿（Extrapolation）

統計モデルを用いて、Positivity違反が生じている層のデータを補完する方法です。

以下はExtrapolationのイメージ図です。観測されているデータから観測されていないデータを推定してデータを補完している様子を表しています。

「存在しないデータを勝手に生成してしまっていいの!?」と疑問を持たれるかもしれませんが、適切な統計モデルを用いることで不可能なことではありません。

もちろん、Extrapolationによる対応が妥当であるか慎重な吟味が必要ですし、トリミングで対処すべきケースもあることでしょう。このあたりのお話はとても発展的な内容になりますのでこの記事では割愛します。

5．まとめ

この記事では、因果推論の識別３条件のひとつ「Positivity」について解説してきましたが、いかがだったでしょうか？

Positivityは因果推論において必要不可欠な条件であり、Positivity violatios（Positivity違反）が生じると、適切に因果効果を推論することが難しくなることがよくご理解いただけたと思います。

最後に今一度、Positivityの重要ポイントを要約しましょう。

①観察研究ではPositivity violationsが十分に起こり得ること

②傾向スコア等でデータの分布をよく吟味してPositivity violationsを確認する必要があること

③Positivity violationsへの対処として、TrimmingやExtrapolationといった方法があること

これから皆さんが因果推論の発展的な内容を学んでいく上で、因果推論の識別３条件（Exchangeability、Consistency、Positivity）の考え方が知識の基盤となっていきます。

ぜひ、mMEDICI Libraryの解説と共に、因果推論の学びを深めていきましょう。

参考文献

• Hernán MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC ．https://static1.squarespace.com/static/675db8b0dd37046447128f5f/t/677676888e31cc50c2c33877/1735816881944/hernanrobinsWhatIf2jan25.pdf

• Yaqian Zhu，Rebecca A Hubbard（2021）　Core Concepts in Pharmacoepidemiology: Violations of the Positivity Assumption in the Causal Analysis of Observational Data: Consequences and Statistical Approaches．Pharmacoepidemiol Drug Saf. 2021 Aug 24;30(11):1471–1485.https://pmc.ncbi.nlm.nih.gov/articles/PMC8492528/

参考図書：『Causal Inference: What If』

Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。

mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。

mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る｜ 無料体験に申し込む

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？-