
【疫学専門家監修】測定バイアスを徹底解説 -ズレたメジャーが、結果を歪める- ゼロから学ぶ因果推論 vol.15
2025.07.31
シリーズ紹介|ゼロから学ぶ因果推論
「医学研究は難しい」、きっと多くの方がそう感じているでしょう。
因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。
因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。
「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。
はじめに
「治療や暴露」と「結果」との因果関係を正しく推論するためには、正しく測定されたデータを用いることが不可欠です。
しかし、データを「正しく測定する」ということは、現実ではとても難しい課題です。
例えば、「患者が薬Aを飲んだと言っていたけれど、実際には飲んでいないかもしれない。」「機器のエラーで、血液データの数値が誤っているかもしれない。」といった、データを測定するときに起こる誤り、すなわち「測定誤差」が生じる可能性が、常につきまとっているのです。
測定誤差は、目に見えにくいものでありながらも、因果推論の結果を大きく歪めてしまう可能性があります。
本記事では、「測定されたデータが、真の値とは異なることで生じるバイアス」である測定バイアス(measurement bias)について、因果推論における考え方に基づきながら、図や具体例を交えてわかりやすく解説していきます。
mMEDICI Library | ひらけ、叡智の扉
叡智の扉を、全ての人が開けるように——。
学びは、限られた豊かな人々だけの特権ではありません。
経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。
mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。
隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。
「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。
この記事のまとめ
この記事を読むと分かること
測定バイアスとは何か
測定誤差の構造
交絡因子における測定誤差
この記事は誰に向けて書かれているか
因果推論を学び始めた初学者の方
測定バイアスを初めて学ぶ方
測定誤差を考慮してDAGを描きたい方
因果推論シリーズ
vol.1:因果推論の出発点 - 因果と関連の違いとは? -
vol.2:因果効果の基本を徹底解説 - Individual Causal Effect(個人因果効果)とAverage Causal Effect(平均因果効果)の違いとは? -
vol.3:初心者のためのTarget Trial Emulation(TTE)
- Part 1 ; ETAFOCAフレームワークについて
- Part 2 ; 三つの時点で考えるバイアスとその対処法
- Part 3 ; 論文の実例で理解を深めるTTEvol.4:Exchangeability(交換可能性)を徹底解説 - Randomization(ランダム化)が実現する因果推論の必須条件 -
vol.5:Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.6:Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.7:Consistency(一致性)を徹底解説 - 観測データと反事実アウトカムを一致させよ -
vol.8:Positivity(正値性)を徹底解説 - 因果推論の落とし穴を回避せよ -
vol.9:Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
vol.10:効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか? -
vol.11:交互作用を徹底解説 - 複数の介入による相乗効果 -
vol.12:DAGを徹底解説
vol.13:交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
vol.14:選択バイアスを徹底解説 - 消えた患者が結果を歪める?-
vol.15:測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める - (本記事)
執筆者の紹介
氏名:平山 優花
所属:専修大学大学院文学研究科心理学専攻修士課程
自己紹介:大学院は臨床心理学を専攻し、公認心理師・臨床心理士の資格取得を目指して、医療機関や児童養護施設等での実習を通じ、様々な領域における心理的支援について学んでいる。障害の有無にかかわらず全ての人が、個々にとっての豊かな社会参加ができる社会の実現を目指し、研究と臨床双方の側面から取り組んでいる。必要な支援を必要としている人に適切に届けるために公衆衛生学と心理学の知見を橋渡しできる力をつけたいと思い、mJOHNSNOWで学びの機会を作っている。
編集者
氏名:菊池祐介
所属:mMEDICI株式会社
専門性:作業療法学修士。首都大学東京(現東京都立大学)・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。
監修者
氏名:廣瀬直紀
所属:mMEDICI株式会社
専門性:保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。
1.測定バイアスとは
測定バイアスとは、「測定誤差に起因するバイアス」を意味します。
そして、測定誤差とは、「治療とアウトカムの関連が、測定過程により歪むこと」と定義されます。
このように定義だけを聞いても、少し抽象的な言葉で分かりづらいですね?
さっそくですが、それぞれ簡単な具体例を用いながら考えてみましょう。
測定誤差の具体例
具体例として、以下のような研究を考えてみます。
「コレステロール低下薬A(以下、薬A)の使用」が「肝疾患Yのリスク」に与える効果を推定したい。
この時、次のようなことが起こる可能性について考えてみましょう。
・医師が、患者に薬Aを処方したことを、電子カルテに記載し忘れた。
・患者が、処方された薬Aを「服用していない」にも関わらず、「服用した」と報告していた。
上記の状況が生じていた場合、「薬Aの使用」が、「正確に測定されている」と言うことはできませんね。
では、正確に測定できていなければ、そのデータを元に因果効果を推論をすることはできないのでしょうか?
たしかに、多くの場合において、あらゆるデータは「完璧な精度で、正確に測定することは困難」です。しかし、その前提の上で、DAGを用いて因果関係を慎重に見極めていくことが大切です。
この状況をDAGを用いて表現すると以下のような図になります。

図中の記号の意味を確認していきましょう。
・A:“真の”薬Aの使用
例)“実際の”薬Aの使用
つまり、 A は「薬Aの使用」の事実そのものを表します。
・A* :“測定された”薬Aの使用
例)“電子カルテに記載された”薬Aの使用記録
(あくまでも、電子カルテ上の記録にすぎない)
つまり、 A* は「薬Aの使用」の指標(記録)に過ぎません。
・U_A: A 以外 の、 A* の値を決定するすべての要因
例)電子カルテにおける、薬Aの使用の「記録漏れ」
この「記録漏れ」によって A* の値が変わる(誤差が生じる)ことになります。
(本来は A* = 1 であるのに、 A* = 0 になってしまう。)
この時、 U_A は「治療変数Aの測定誤差」と呼ばれます。
そして、このような U_A(治療変数Aの測定誤差)に起因して生じるバイアスが、「測定バイアス」です。
因果推論では、正確に測定できていない可能性があるという前提のもと、データには「真のデータ」と「測定されたデータ」があると捉え、因果効果の推論を進めていきます。

2.測定誤差の構造
次に、「測定誤差の構造」の種類を見ていきます。
測定誤差における、 A 、 A* 、 UA 、 Y 、 Y* 、 UY の関係を、「測定誤差の構造」と呼びます。
「測定誤差の構造」は、次の二つの軸によって四つに分類することができます。
「独立性(Independence)」
「非差異性(Non-differentiality)」

これらの「独立」「依存」「差異」「非差異」について、それぞれが何を意味しているのか見ていきましょう。
①「独立」について
「独立」とは、 U_A(治療変数Aの測定誤差)と U_Y(目的変数Yの測定誤差)が独立している状態を意味します。
「独立」の構造を持つ測定誤差を表したDAGの例が以下です。

「独立」の構造を持つ測定誤差の具体例を考えてみましょう。
「薬Aの使用」と「肝疾患Y」に関する情報がそれぞれ、「データ入力の誤りがランダムに発生している電子カルテ」から取得される場合などがあります。
U_A: A*(測定された薬Aの使用)における、データ入力の誤りによる誤差
U_Y: Y*(測定された肝疾患Y)における、データ入力の誤りによる誤差
この時、 U_A と、 U_Y は、それぞれにおいてランダムな要因によって生じた誤差であり、それぞれが「独立している」と言えます。
②「依存」について
「依存」とは、 U_A(治療変数Aの測定誤差)と U_Y(目的変数Yの測定誤差)が、共通の要因に依存する状態を意味します。
「依存」の構造を持つ測定誤差を表したDAGの例が以下です。

「依存」の構造を持つ測定誤差の具体例を考えてみましょう。
「薬Aの使用」と「肝疾患Y」に関する情報が、研究参加者に対する電話インタビューにより事後的に収集される場合などがあります。
U_AY:研究参加者個人の記憶力
この時、 U_AY(研究参加者個人の記憶力)は、 U_A(治療変数Aの測定誤差)と U_Y(目的変数Yの測定誤差)の共通の要因です。
結果として、 U_AY(研究参加者個人の記憶力)が「治療A」と「結果Y」の双方の測定に影響を与えることが推測されます。
このように、 U_A(治療変数Aの測定誤差)と U_Y(目的変数Yの測定誤差)が、共有の要因U_YA に依存している関係性を、「依存」の構造と言います。
③「差異」について
「差異」とは「 A(“実際の”治療A)が U_Y(結果変数Yの測定誤差)に影響を与える」、あるいは「 U_Y(目的変数Yの測定誤差)が A(“実際の”治療A)に影響を与える」状態を意味します。
「差異」の構造を持つ測定誤差を表したDAGの例が以下です。

「差異の構造」を持つ測定誤差の例について考えてみましょう。
医師が「薬Aの使用」が「肝疾患Y」を引き起こすと疑い、薬Aが投与された患者には「肝疾患Yがあるかもしれない」とより注意深く診断を行なったとします。
U_Y:医師による診断の注意深さの違いによって生じる、結果Yの測定誤差
この時、「薬Aの使用の有無」によって「肝疾患Y」の診断精度が異なるかもしれません。つまり、 A(“真の”薬Aの使用)が U_Y に影響を与えることが推定されます。このように生じる測定誤差の構造を、「差異」の構造と言います。
④「非差異」について
「非差異」とは、 A(“真の”薬Aの使用)が U_Y(結果変数Yの測定誤差)に影響を与えない、かつ U_Y(結果変数Yの測定誤差)が A(“真の”薬Aの使用)に影響を与えない状態を意味します。
「非差異」の構造を持つ測定誤差を表したDAGの例が以下です。

「非差異の構造」を持つ測定誤差の例について考えてみましょう。
「薬Aの使用」と「肝疾患Y」に関する情報がそれぞれ、「データ入力の誤りがランダムに発生している電子カルテから取得される場合」などがあります。
U_Y: Y*(測定された肝疾患Y)における、データ入力の誤りによる誤差
この時、A(真の薬Aの使用)は測定誤差U_Y に影響を与えず、その逆も起こらないと推定されます。ここで生じる測定誤差は、「非差異」の構造を持ちます。
「測定誤差の構造」の例を「独立 - 依存」「非差異 - 差異」の2軸で区分すると以下のようになります。

3.測定誤差によって生じるバイアス
測定誤差によって生じるバイアスは、文脈によって「Recall bias(想起バイアス)」や「Reverse causal bias」と呼ばれることがあります。
①Recall bias(想起バイアス)の例
Recall bias(想起バイアス)は、参加者が過去の治療Aを正確に思い出せないことで、誤った情報が収集されることで起こるバイアスです。
例えば、ある研究者が、「薬A」が「認知症Y」に与える影響を検証したいと考えたとします。
そして、「薬Aの使用」についてのデータを、参加者本人に対する面接によって収集した場合を想像してみましょう。
Y:“真の”認知症の有無
A:“真の”薬Aの使用
A*:患者の報告による薬Aの使用
U_A:参加者の記憶能力によって生じる、「治療Aの使用」の誤差
この時、 A* は U_A の影響を受けると同時に、 Y は、 U_A に影響を与えることが推定されます。この状況をDAGを用いて表すと以下のようになります。
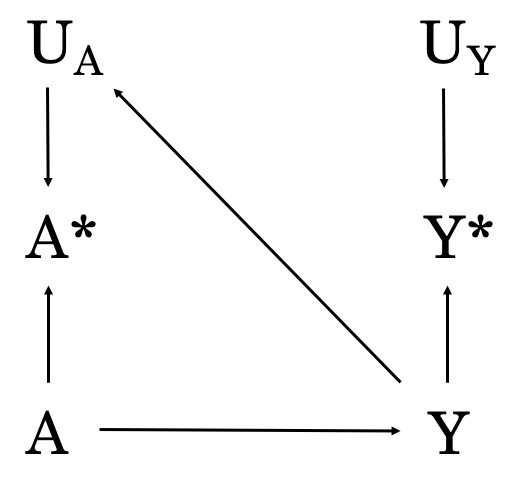
このように、「結果変数Y(認知症)」が U_A(A*における測定誤差)に影響を与えることによって生じるバイアスを、Recall bias(想起バイアス)と呼びます。
②Reverse causation biasの例
Reverse causation biasは、本来の因果関係( A → Y )を評価したいのに、 Y が A の測定に影響を与えることによって、誤った因果関係が推定されるバイアスです。
例えば、ある研究者が、「コレステロール低下薬A(薬A)の使用」が、「肝疾患リスクYに与える影響」を検証したいと考え、「薬Aの使用」の指標として A*(薬Aの血中濃度)をデータを収集した場合を想像してみます。
Y:“真の”肝疾患リスク
U_A:A*(薬Aの血中濃度)に影響する要因による、薬Aの測定誤差
この時、「肝疾患Y」があると A*(薬Aの血中濃度)が変化する可能性があります。つまり、 Y(“真の”肝疾患リスク)は、 U_A(薬Aの測定誤差)に影響を与えることされます。
この状況をDAGを用いて表すと以下のようになります。

このように「“真の”結果の値Y」が「治療の測定誤差U_A」に影響を与えることによって生じるバイアスは、「Reverse causation bias」と呼ばれます。
このように、測定誤差の構造をDAGによって整理し、測定バイアスが生じるメカニズムを理解することが大切です。
4.交絡因子の測定誤差
「交絡因子の測定誤差」とは
交絡因子においても、測定誤差が生じることがあります。
交絡因子とは、「原因と結果の両方に影響を与える第三の変数」を意味します。
交絡因子についてはこちらので記事で詳細に解説しています。
【疫学専門家監修】交絡を徹底解説 - 結果を歪める、因果推論の最重要課題
「交絡因子の測定誤差」の具体例を見てみましょう。
例えば、ある研究において「肝炎既往歴Lを有する個人は、肝疾患Yを発症する可能性が高い。また、肝臓への負担を考慮して、コレステロール低下薬A(以下、薬A)を処方される可能性が低い」という仮説を立て、質問紙調査を用いてデータを収集しようと考えたとします。
A:“真の”薬Aの使用(“真の”治療因子)
Y:“真の”肝疾患の発症リスク(“真の”結果因子)
L:“真の”肝炎既往歴(“真の”交絡因子)
L*:“測定された”肝炎既往歴(“測定された”交絡因子)
この仮説をDAGを使って描くと、以下のようになります。

このようなデータ収集を行った際、次のようなことが起こる可能性はないでしょうか?
・一部の研究参加者が、肝炎既往歴を思い出せず、誤った記憶のもと回答を行う
・一部の研究参加者が、既往歴を他人に知られたくないと思い、不正確な回答を行う
もし上記が起こっていた場合、 L*(測定された肝炎既往歴)には誤差が含まれていることが推測されます。
これを、「交絡因子の測定誤差」と呼びます。
「交絡因子の測定誤差」がもたらす「見かけの効果修飾」
交絡因子の測定誤差は、「見かけの効果修飾」と呼ばれる効果を引き起こすことがあります。
効果修飾(Effect modification)とは、「治療A」が「アウトカムY」に与える因果効果が、「共変量L」のレベルに応じて変化することを意味します。
効果修飾について詳しく知りたい方は、こちらの解説記事をご覧ください。
【疫学専門家監修】効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか?
「交絡因子の測定誤差」がもたらす「見かけの効果修飾」について、具体例をもとに考えてみましょう。
「 L* = 1(肝炎の既往歴を報告した研究参加者)」の全員が肝炎既往歴を有し、また「 L* = 0(肝炎の既往歴を報告しなかった参加者)」の 1/3 が、実は肝炎の既往歴を有している( L = 1 )という状況を想定してみます。
この時、「交絡因子L(肝炎既往歴)の“真の値”」と「測定された交絡因子L*(報告された肝炎既往歴)」は、「 L* = 1」の人たちでは一致しますが、「 L* = 0」の人たちでは一致しません。

それでは、 L*(報告された肝炎既往歴)で層別化して「薬A」による「肝疾患リスクY」の効果を調べたい時に、「 L* = 0(肝炎既往歴なしと回答)のグループの中に、実は L = 1(肝炎既往歴あり)の人が含まれている」ことを研究者が認識していなかった場合、どのようなことが起こり得るでしょうか?
ここでは、「コレステロール低下薬A(薬A)」は「肝疾患Yの発症リスク」に効果がない、という前提で考えていきましょう。
L* = 1 のグループ
全員が「肝疾患の既往あり」
そのため、A=1(薬Aを投与)と A=0(投与なし)とで肝疾患リスクYの差がない
L* = 0 のグループ
「肝疾患既往あり」と「肝疾患既往なし」の人がどちらも含まれる。
例えば、 A = 1(薬Aを投与)のグループに「肝疾患既往あり」の人が多く含まれる時、肝疾患リスクがより高くなるかもしれません。
その結果、 A = 1(薬Aを投与)と A = 0(投与なし)とで肝疾患リスクYの差が生じる可能性があります(薬Aの投与によって肝疾患リスクが高まるように認識してしまう)。
このように、「 L* = 1 では薬Aは肝疾患リスクに効果がない」、「 L* = 0 では薬Aが肝疾患リスクを高める」と解釈してしまい、L*の層(1、0)で薬Aによる肝疾患リスクYが異なることから、「 L* は薬Aと肝疾患リスクYの効果修飾因子である」と結論づけてしまう可能性があります。
このような現象を、「交絡因子の測定誤差」による「見かけの効果修飾」と呼びます。
5.測定誤差とDAG
一般的にDAG表記が行われる場合、そこにはある暗黙の仮定があります。
それは、「DAG上のすべての変数は、完全に測定されている」という仮定です。
しかし、これまで本記事で見てきたように、実際には、全ての変数が完全に測定されているわけではありません。
そのため、時に「DAG上のすべての変数は、完全に測定されている」という仮定を暗黙的に用いることは、誤った結論を導くことに繋がります。
では、どうすればよいのでしょうか?
Causal Inference: What If.(2020)では、目的に応じて描き分けることが推奨されています。
目的に応じた描き分けをする際の考え方の一つに、以下のような2段階アプローチがあります。
2段階アプローチ
Step1:測定誤差を考慮しないDAG(交絡バイアスと選択バイアスの検討に焦点を当てる場合)
Step2:測定誤差を明示したDAG(変数の測定値と真の値を区別して検討する場合)

このように、目的に応じてDAGを使い分け、測定誤差について慎重に検討する姿勢が大切です。
6.まとめ
本記事では、「測定バイアス」について、その要因となる「測定誤差」が起こる構造や、測定誤差にバイアスが生じるメカニズムについて解説してきました。
治療や結果、または交絡因子といったあらゆる変数において「測定誤差」が起こり得ることを常に念頭におきながら、DAGを用いて丁寧に因果推論を進めることが大切です。
ゼロから学ぶ因果推論シリーズでは、これまでに交絡バイアス、選択バイアス、Immortal time bias についても解説してきました。因果関係の推論を歪めるさまざまなバイアスについて知識を整理し、因果推論について理解を深めていきましょう。
ゼロから学ぶ因果推論シリーズ 「バイアス」関連記事
・交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
・選択バイアスを徹底解説 - 消えた患者が結果を歪める?
・Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
参考図書:『Causal Inference: What If』
Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。
mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。
因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。
そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。
mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。
本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです!
・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ(ex. RWDピア)
・24時間利用可能なオンライン自習室「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください!
・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催【YouTubeラジオコンテンツ 耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。
すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。
シリーズ一覧
因果推論シリーズ
vol.1:因果推論の出発点 - 因果と関連の違いとは? -
vol.2:因果効果の基本を徹底解説 - Individual Causal Effect(個人因果効果)とAverage Causal Effect(平均因果効果)の違いとは? -
vol.3:初心者のためのTarget Trial Emulation(TTE)
- Part 1 ; ETAFOCAフレームワークについて
- Part 2 ; 三つの時点で考えるバイアスとその対処法
- Part 3 ; 論文の実例で理解を深めるTTEvol.4:Exchangeability(交換可能性)を徹底解説 - Randomization(ランダム化)が実現する因果推論の必須条件 -
vol.5:Standardization(標準化)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.6:Inverse Probability Weighting(逆確率重み付け)を徹底解説 - 交絡調整の基本をわかりやすく図解 -
vol.7:Consistency(一致性)を徹底解説 - 観測データと反事実アウトカムを一致させよ -
vol.8:Positivity(正値性)を徹底解説 - 因果推論の落とし穴を回避せよ -
vol.9:Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -
vol.10:効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか? -
vol.11:交互作用を徹底解説 - 複数の介入による相乗効果 -
vol.12:DAGを徹底解説
- 基礎編;因果推論の必須ツールで交絡因子を可視化する
- 応用編;調整してはならない?コライダーと媒介変数の落とし穴
vol.13:交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -
vol.14:選択バイアスを徹底解説 - 消えた患者が結果を歪める?-
vol.15:測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める - (本記事)
©mMEDICI Inc. ALL RIGHTS RESERVED.



















