【疫学専門家監修】ランダム誤差を徹底解説 -研究結果は「運」で歪むのか？vol.16

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに

因果推論の目標は、「ある介入がアウトカムをどれくらい変えるのか」を推定することです。

ただ、私たちが手にできるのは「現実的に収集できる限られたデータ」だけです。データの偏りや偶然の“ゆらぎ”のせいで、結果には必ず不確実性がつきまといます。

本記事では、不確実性の原因の一つである「ランダム誤差」に焦点を当て、その構造や原因、標準誤差や信頼区間による表し方を解説します。

さらに、スーパー母集団（super-population）という概念を通じて、推定値がどの集団の効果を表しているのかを明確にする重要性についても考えていきます。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• ランダム誤差とは何か - 系統誤差との違いと、その二つの発生原因を理解する

• 標準誤差と信頼区間 - 推定の不確実性を正しく表現し、解釈するための基本を身につける

• 推定の背景にある「仮定された集団」 - 誰に対する効果なのかを見失わずに解釈する視点を養う

この記事は誰に向けて書かれているか

• 症例数や偶然の影響で研究結果がどの程度変わるのかを理解したい方

• 信頼区間を「なんとなく」ではなく根拠を持って解釈・説明できるようになりたい方

• 臨床研究の結果を目の前の患者や現場の判断にどう生かせるかを考えたい方

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

• vol.15：測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める -

• vol.16：ランダム誤差を徹底解説 -研究結果は「運」で歪むのか？（本記事）

執筆者の紹介

氏名：KA
所属：病院勤務
自己紹介：薬剤師。大学卒業後、調剤薬局およびドラッグストアでの服薬支援を通じて地域医療に携わる。出産・育児を機に一時離職後、薬学的専門性をより幅広く発揮できる環境を求め、整形外科病院でキャリアを再開。臨床での疑問を解決するため、エビデンスを正しく解釈する力を身につけたいと考え医学研究オンラインスクールmJOHNSNOWに入会。疫学や医学研究の基礎を体系的に学びつつ、得た知見を実践に活かすべく日々の業務に取り組んでいる。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。

１．ランダム誤差とは何か

定義

ランダム誤差とは、「推定値が真の値からずれる要因」の一つです。

そもそも「推定値が真の値（因果効果）からずれる」とはどういうことでしょうか？

私たちが研究を行う時、多くの場合に本当に知りたいのは「研究集団での効果」ではなく、「より大きな母集団での効果」です。

例えば、とある病院で糖尿病患者に対する治療薬の効果を調べる時には、「〇〇病院における糖尿病患者に対する治療薬の効果」から「日本中のすべての糖尿病患者に対する治療薬の効果」を“推定”することが目的と言えます。

このように、限られたサンプル（とある病院の患者データ）から、母集団すべて（日本中の糖尿病患者）における「真の値（糖尿病治療薬の真の因果効果）」を推定する時、「推定値」と「真の値」は必ずしも一致しません。

この「推定値」と「真の値」の差の原因は、研究デザインの設計等によって生じる「系統誤差」と、偶然によって生じる「ランダム誤差」と、の大きく二つに分けられます。

ランダム誤差と系統誤差の違い

「推定値」と「真の値」の差の原因となる、この二つの誤差「系統誤差」と「ランダム誤差」について解説していきます。

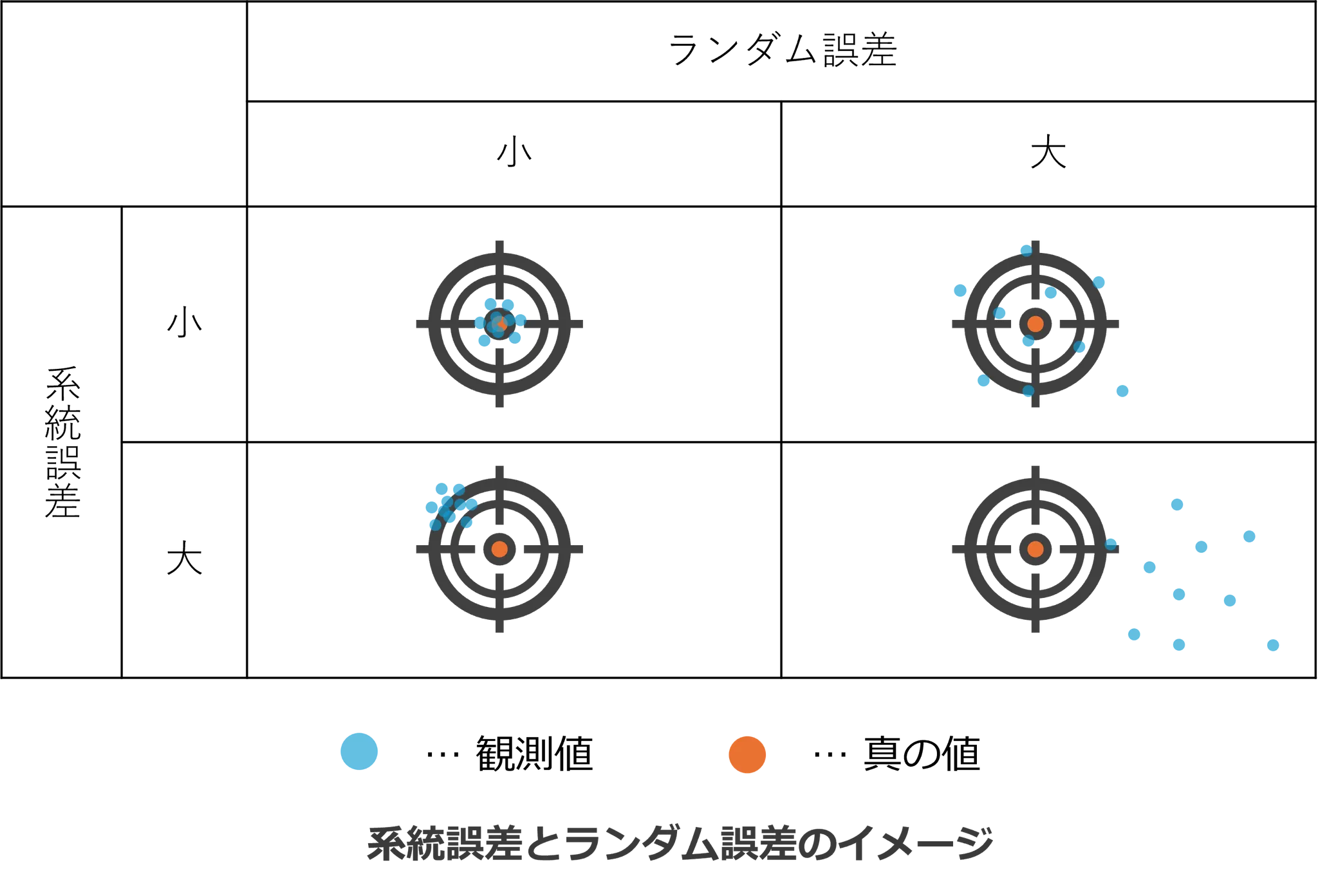
【用語の整理】
実際に収集された調査結果と真実との間にある差を誤差という。
誤差は、理想的な状況でも偶然に起こるものと、データの収集方法が適切でないため系統的に起こる一定の方向性を持つものに分けられ、前者を偶然誤差、後者を系統誤差という（日本疫学会　疫学用語の基礎知識　偶然誤差　系統誤差より）。

系統誤差は、データの収集方法などの設計上の原因によって系統的に生じる一定方向の誤差です。具体的には次のような例があります。

• 交絡（Confounding）
  検診の効果を評価する研究で、検診を受ける人ほど健康意識が高く、運動や食事管理などの生活習慣も整っているとします。
  この場合、「検診を受けること」と「アウトカム（健康状態）」の間に健康志向という交絡因子が存在し、検診の効果を過大評価する原因になります。

交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• 選択バイアス（Selection bias）
  副作用の強い薬剤の試験では、試験終了時の治療群に「副作用に耐えられた健康な人」だけが残る可能性があります。
  その結果、本来の治療効果よりも過小評価または過大評価される恐れがあります。

選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

• 測定バイアス（Measurement bias）
  患者に薬の副作用について後からアンケートを取った場合、既に副作用を経験していた人の方が「原因はあれかもしれない」と記憶を辿って、暴露歴を詳細に報告しやすくなります。

測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める -

系統誤差は、何度試行を繰り返してもその差の方向性や大きさが変化しません。ゼロ点がずれた体重計をイメージすると分かりやすいでしょう。


一方、ランダム誤差は、系統誤差が排除された理想的な状況であっても偶然によって生じます。個人の運や未知の因子によって生じるこの揺らぎは、毎回異なり予測ができません。

こうした偶然の揺らぎによる不確実性こそが、ランダム誤差です。

推定結果を正しく解釈するためには、系統的バイアスを排除してなお残る「ランダム誤差」という不確実性を理解することが不可欠です。

２．ランダム誤差の二つの原因

ランダム誤差には、大きく二つの原因があります。

1. サンプリング変動（Sampling variability）

2. 非決定的反事実的結果（Nondeterministic counterfactuals）

サンプリング変動（Sampling variability）

一つ目はサンプリング変動です。

皆さんも、「 n が小さいので判断できない」「 n ＝ 1 の経験ですが」といった表現を耳にしたことはありませんか？

これらは、サンプリング変動という考え方と深く関係しています。

サンプリング変動とは、全体集団（母集団）から一部をランダムに取り出すことを繰り返した時、平均値やリスク差、リスク比などの統計量がサンプルごとに異なることを指します。


サイコロを振った時の出た目の平均値を考えてみましょう。
１～６の目が出る確率がすべて等しい六面サイコロを振った時の期待値は3.5です。

それでは、実際にこのサイコロを１回、10回、100回、10000回振った時、それぞれの平均値はどのようになるでしょうか？


ここでは、特別なソフトウェアのインストールなしに、Google Chromeなどのブラウザ上でデータ分析を実行できる myCompiler を使用して、実際に確認してみましょう。

まずはこちらリンクから myCompiler へアクセスし、以下の手順に沿って分析を実行してみましょう。

import random
def dice_average(n_trials):
    results = [random.randint(1, 6) for _ in range(n_trials)]
    return sum(results) / n_trials
# 各試行回数での平均を計算
for trials in [10, 100, 10000]:
    avg = dice_average(trials)
    print(f"{trials}回振った平均: {avg:.3f}")

理論上は、期待値の3.5に等しくなるはずですが、繰り返し実施したときの平均値は少しずつ異なる値となることがわかります。

実際にシミュレーションしたときの結果

10回振った平均：3.70
100回振った平均：3.60
10,000回振った平均：3.51

このようなばらつきこそがサンプリング変動です。

サンプリング変動は標準誤差という形で表されますが、この詳細については後程ご紹介します。


また、サイコロを振る回数が多いほど、出た目の平均値は期待値の3.5に近づきます。

サンプリング変動はサンプル数を増やすことでその影響を抑えることができるのです。

裏を返せば、サンプル数が少ないと推定値が真の値から大きく外れる可能性があるということです。

このように、ランダム誤差の性質から、本当は死亡率が57％の母集団であっても、十分なサンプルが確保できず10人だけを抽出して死亡率を計算すると50％という結果が導かれ、死亡率を過小評価してしまうかもしれません。

非決定的反事実的結果（Nondeterministic counterfactuals）

ランダム誤差のもう一つの原因は、非決定的反事実的結果です。

一見して難解そうな用語ですが、簡単に言い表すと「個人がある介入を受けた時の結果は、確定したものではなく、確率的に定まっている」ことを意味します。

例えばAさんが心臓移植を受けた時、「必ず完治する」とは限らずに「90％の確率で完治する」といった確率的な結果になることがあります。運や未知の要因によって個人ごとに完治の確率は異なり、Bさんは60％、Cさんは85％かもしれません。

このように、反事実的結果が「個人ごとの確率分布」として定義される場合、これを非決定的反事実的結果と呼びます。

このような不確実性は、サンプルサイズをいくら増やしても解消されません。なぜなら、個人ごとの運や未知の要因によるばらつきは、根本的に確率的なものであるためです。

反事実的結果 といった因果推論の基本概念はこちら
因果効果の基本を徹底解説 - 個人因果効果と平均因果効果の違いとは？

３．識別（Identification）と推定（Estimation）の区別

私たちが知りたい「真の因果効果」というものは、多くの場合、現実のデータから直接計算することはできません。

例えば、薬剤Aを使用した時の５年後の生存率を知りたいと考え、自施設の患者さんたちからデータを集め研究を行ったとします。

この時に私たちが本当に知りたいのは、おそらく「研究対象となった自施設の患者さん」における効果ではなく、「今後この薬を使う未来の患者さん」における効果でしょう。

しかし、未来の患者さんたちに薬を使用した場合のデータを集めることは不可能です。現実では「研究対象となった自施設の患者さん」から得られたデータを活用するしか方法はありません。

現実世界の様々な制約のもとに集められたデータを用いて「真の因果効果」に近づくためには、「識別」と「推定」という二つのステップを踏む必要があります。

識別とは？

「識別（identification）」とは、すなわち観測データから反事実的な因果効果を理論的に導けるかどうかを確認することです。

識別が可能な状態とは、「一貫性（consistency）」「正値性（positivity）」「交換可能性（exchangeability）」の三条件が満たされている状況です。

詳細については過去の記事をご参照ください。

・Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ
・Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ
・Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）により実現する因果推論の必須条件

推定とは？

識別が可能であれば、次は「推定（estimation）」の段階です。

推定とは、実際のサンプルデータを使って因果効果を数値として算出する作業です。

無限大のサンプル（母集団全体）を研究対象とする場合には、理論上ランダム誤差が問題とならないため、識別三条件が成立すれば因果効果を直接計算することが可能です。

しかし、実際の研究では母集団から有限のサンプルデータを集めることとなります。
有限であるがゆえに、どれほどよくデザインされたランダム化比較試験であっても、推定値はランダム誤差を伴います。

そのため、私たちは推定値に不確実性を表す統計量（例えば標準誤差やそれに基づく信頼区間）を付け加えることで、真の因果効果を「範囲」として表現し、解釈します。


このように、識別とは「観測データから因果効果を理論的に導けることを保証する“前提条件”」であり、推定とは「実際のサンプルデータを使って因果効果の大きさを数値として求める作業」です。

つまり「推定」は、「識別条件」が成立して初めて意味を持つと言えるのです。

４．推定の不確実性をどう表現するか

推定に伴う不確実性を表す方法として、「標準誤差」と「信頼区間」があります。

それぞれについて丁寧に解説していきましょう。

標準誤差

標準誤差は、サンプリング誤差による推定値の「ばらつきの大きさ」を数値化したものです。

「たった１回のデータから、なぜばらつきが分かるのか？」と不思議に思うかもしれません。

しかし、あるサンプルの一つ一つのデータが「平均」からどれだけ離れているか（ ＝ 標本標準偏差）を見れば、他のサンプルから計算した平均がどれだけ変動するかを予想することができるのです。


標準誤差は次のような式で表されます。突然、難しそうな数式が登場して驚かれた方もいるかと思いますが、心配ありません。計算する必要はありませんので、「この数式がどのような意味をもっているのか」に注目して、標準誤差の性質について考えてみましょう。

分子の数式は難しく思えますが、詳しく読み解く必要はありません。ここでは分母にあるサンプルサイズの平方根（ √n ）に注目してください。サンプルサイズ（ n ）の値が大きくなるほど、√ n の値も大きくなりますね？

つまり、標準誤差の計算式からは、サンプルサイズ（ n ）が大きくなるほど分母の値が大きくなり、結果として「標準誤差」の値が小さくなるという性質が理解できます。

信頼区間

推定の不確実性を表現するもう一つの手段が信頼区間です。

信頼区間とは、ランダム誤差によって生じる推定の不確実性を考慮した、推定値の信頼できる「範囲」のことです。

信頼区間の幅はサンプルサイズによって変わり、サンプルサイズが大きくなるほど信頼区間は狭くなります。また、信頼区間は「どのくらいの頻度で真の値を含むか」という基準で妥当性が定義され、一般的によく使われるのは「95％信頼区間」です。

今回は一般的な信頼区間の一つである「ワルド法（Wald method）」を用いた95％信頼区間を想定して話を進めていきます。

95%信頼区間の計算式は次のようになります。

95％信頼区間 ＝ 推定値 ± 1.96 × 標準誤差

この「1.96」という数値は、正規分布の中心95％の範囲をカバーする値です。ここで注意したいのは、正規分布に従うのは「真の値」ではなく、「推定値の分布」であるという点です。

推定値は試行ごとにばらつきますが、十分なサンプルサイズなどの条件を満たすと、このばらつきは真の値を中心とする正規分布で近似できることが知られています。

この性質を利用し、推定値 ± 1.96 × 標準誤差の範囲で95％信頼区間を繰り返し作ったとき、95％の区間は真の値を含むように設計されています。

具体的に理解するために、「薬剤A」を投与した場合の「骨折リスク」を例に考えてみましょう。

薬剤Aを服用した13人のうち７人に骨折が発生したとします。

この時の骨折リスク（ ＝ 点推定値）は ７ ÷ 13 ≒ 0.5385（ ≒ 53.85％ ）です。

この値は「推定値」であり、「真の骨折リスクそのもの」ではありません。

なぜなら、「サンプリング変動」のパートでご説明した通り、同様の研究を繰り返せば、推定値はばらつくことでしょう。

私たちはあくまで有限のサンプルから情報を得ており、母集団の真の値には不確実性を伴ってしか近づけないのです。

この不確実性を、ここでは95％信頼区間で表してみたいと思います。

今回の例では、「骨折するかしないか」という二項分布に従う確率pを推定しているため、標準誤差は以下のように計算されます。

標準誤差 ≒ √{（7/13）×（6/13）÷ 13 } ≒ √（ 0.007645 ） ≒ 0.138

これをもとに、95%信頼区間を計算すると次のようになります。

0.5385 ± 1.96 × 0.138 = 0.5385 ± 0.2705
= [0.268, 0.809]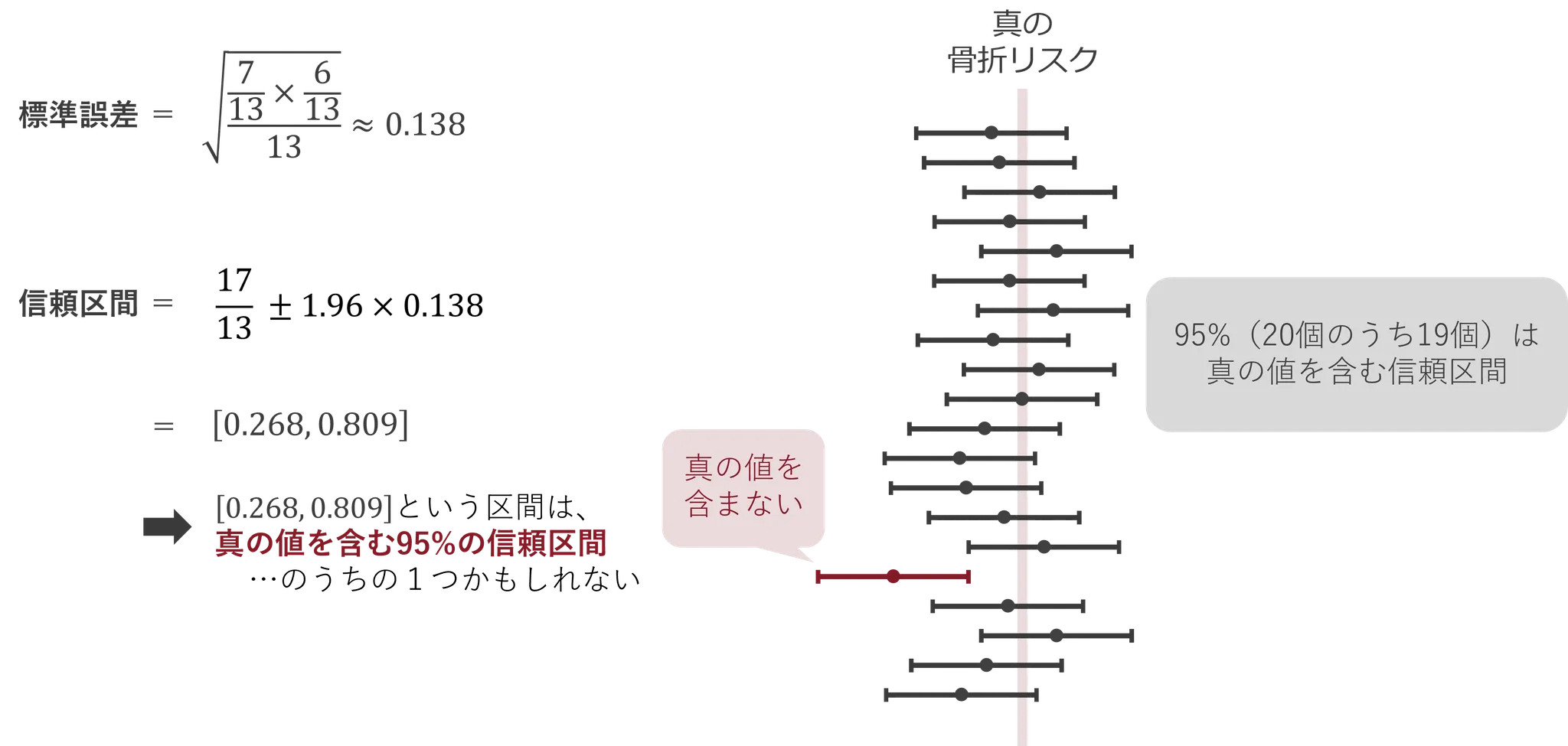

95％信頼区間は、もし私たちが同じ方法で100回調査を繰り返して毎回信頼区間を計算したとしたら、そのうちの95個の区間が真の骨折リスクを含むように設計されています。

つまり、今回得られた信頼区間［ 26.8％，80.9％ ］も、その「真の値を含む区間の一つである可能性が高い」と考えることができます。


よくある誤解に「信頼区間が真の効果を含む確率が95％だ」というものがありますが、真の効果は「変動するもの」ではなく、あくまで固定された未知の値です。

つまり、一つの信頼区間は、真の因果効果を「含む」か「含まない」かのどちらかになります。

このように、信頼区間は因果効果の推定値に対する不確実性を伝える便利なツールではありますが、その解釈を誤ると推定結果を過信してしまうリスクがあります。

因果推論では、「推定値 ± 不確実性」を明確に示し、その上で結果を慎重に解釈することが不可欠です。

５．スーパー母集団（super-population）とは？

これまで、私たちは「母集団からランダムにサンプルを取って推定する」という考え方を前提にしてきました。ここでは、その「母集団」に改めて焦点を当て考えてみましょう。

私たちが「母集団」について考える時、しばしば “同様の患者が無限に続く仮想の集団”＝スーパー母集団 を仮定します。そして研究サンプルは、そのスーパー母集団からランダムに１回抽出された標本とみなします。

３章の「識別と推定」の説明でも触れましたが、自施設の患者データを使用していたとしても、私たちが本当に知りたいのは、多くの場合「研究対象となった患者に効果があったかどうか」ではなく、「今後この薬を使う未来の患者に効くかどうか」です。

このように、私たちが無意識に想定している「未来の患者たち」のような、無限に広がる理想的な集団を「スーパー母集団（super-population）」と呼びます。

スーパー母集団を仮定するメリットには、研究で得られた知見をより大きなターゲット集団に一般化することができるということに加えて、統計解析がずっとシンプルになるという点があります。

例えば、ある薬の効果によって「その人が亡くなるか助かるか」が、運や測定できない要因に左右されることがあるとします。つまり結果は“確率的”で、「必ず助かる」「必ず亡くなる」とは限りません。

この時、研究で対象とする患者たちをスーパー母集団からランダムに抽出された人々とみなすことで、「死亡するか生存するかは一定の確率で起こる結果」として整理できます。

そして、この「確率的な結果」をスーパー母集団におけるランダムな現象と考えることで、コイン投げのような現象として扱うことができます。その結果、二項分布などのシンプルな統計モデルを使って解析することが可能になるのです。

解釈の注意点

ただし、スーパー母集団を仮定する際には注意が必要です。

なぜなら、そのままでは 「この推定値はいったい誰のための効果なのか？」 が曖昧になってしまうからです。

スーパー母集団という考え方は便利ですが、因果効果の対象が抽象的になりすぎると、私たちが実際に意思決定をすべき集団、例えば「これから治療を受ける患者さん」との間にずれが生じる可能性があります。

そのため、解析を行う時には、研究対象となった集団と、その集団が属する母集団をはっきり区別することが大切です。

そして、得られた推定値を本当にターゲットとする患者集団に当てはめて良いのかどうか、慎重に検討しなければなりません。

６．決定論的 vs 確率的な反事実

前章では、母集団の仮定をどのようにおくかによって、推定の手法や解釈が変わることについて解説しました。

６章では介入の結果を、「決定論的モデル」と「確率的モデル」のどちらと仮定するかによる推定への影響を見ていきたいと思います。

決定論的モデル

例えば、薬Aを服用すれば100％生存し、服用しなければ100％死亡するといったように、介入の有無によって結果が決まるモデルを「決定論的モデル」と呼びます。

介入結果にランダムな不確実性がなく、不確実性の原因はサンプリング変動のみとなります。

確率的モデル

ところが実際には、同じ条件の患者さんであっても結果は必ずしも同じにはなりません。

薬Aを服用しても「必ず助かる」とは限らず、ある人は90％助かるけれど別の人は70％、さらに別の人は50％といったように、個人ごとに生存確率にばらつきがあるのです。

このように「一人一人の反事実的な結果（もし治療したらどうなるか）が確率的にしか定まらない」と考えるのが確率的モデルです。

このモデルでは、推定の不確実性は２種類あります。

1. サンプリング変動：誰をサンプルに選ぶかによるばらつき

2. 個人レベルのランダム性：運や未知の要因で、その人自身の結果が確率的に決まること

そのため、決定論的モデルよりも一段と不確実性が大きくなるのです。

決定論的モデルと確率的モデルでの平均因果効果の解釈

では、決定論的モデルと確率的モデルを仮定することで、推定はどのように変わるのでしょうか？


１．サンプル内における平均因果効果（研究対象者だけでの平均効果）

・決定論的モデル
各個人が持つ「固定された効果」を平均します。

例：「Aさんには５年延命効果」「Bさんには３年延命効果」…を平均する。

・確率的モデル
各個人が持つ「効果の期待値（平均的な効果）」を平均します。

例：「Aさんが薬を使った時平均すると70％生存」「Bさんは85％」…を平均

つまり、同じデータを使っても「固定値の平均」と「期待値の平均」とで解釈が少し違ってきます。


2. スーパー母集団における平均因果効果（無限に広がる理想的な集団での平均効果）

ここでは話がシンプルになります。決定論的モデルでも確率的モデルでも、推定方法に違いは生じません。つまり、スーパー母集団を仮定すると、個々の患者が持つ効果が「固定された値」か「確率的にばらつく値」かに関わらず、最終的に求めるのは 集団全体の平均 になります。

・決定論的モデル
個人ごとの固定された効果を集めて「母集団全体の平均」をとる。

・確率的モデル
個人ごとの効果が確率的にばらつくとしても、各人の「期待される効果（平均的な効果）」を集めて「母集団全体の平均」をとる。

どちらの考え方でも、最終的には「母集団全体の平均効果」を計算することになり、推定方法は一致します。

不確実性を扱うための実践的なポイント

前述のように、仮定するモデル（決定論的か確率的か）によって、推定値の意味や解釈は変わることがあります。

そのため、研究を計画するときや解析する時には、自分がどのモデルを前提にしているかを明示することが大切です。

また、得られた結果は必ず 「推定値 ± 不確実性」 の形で示しましょう。

さらに、その不確実性がどのように生じているのか（サンプリング変動なのか、個人レベルのばらつきなのか）を説明することで、結果の解釈がずっと明確になります。

最後にもう一つ大事なのは、「この因果効果は誰に対するものか？」 を常に意識することです。

今の推定値が対象にしているのは、観察したサンプルなのか、それともより広い母集団なのかを区別しながら結果を伝えることが必要です。

７．まとめ

本記事ではランダム誤差について解説してきました。

因果推論の目標は、「ある介入がアウトカムをどれくらい変えるのか」を推定することです。

しかし、その推定には必ず不確実性があり、ランダム誤差（偶然による揺らぎ）と 系統的バイアス（設計や測定の偏り）が含まれます。

どんなに丁寧に研究しても、こうした不確実性は避けられません。

だからこそ、「計算された“推定値そのもの”」だけでなく「どのくらい確かな値なのか」もあわせて伝えることが大切です。

そのために、標準誤差や信頼区間といった統計的な指標を用いて、「この推定値にはこれくらいの幅がある」と示すことが大切です。

そしてもう一つ重要なのは、「誰に対する効果を推定しているのか」 を意識することです。

つまり、因果推論とは「推定値」と「その不確実性」をあわせて考え、さらに「誰のための効果なのか」を意識して解釈していくプロセスが重要です。

ランダム誤差を理解した上で、不確実性に正しく向き合い、誠実に伝えることが、研究者にも臨床家にも欠かせない姿勢だと言えるでしょう。

参考文献

・佐々木 敏．わかりやすいEBNと栄養疫学．同文書院 2005
・東京大学教養学部統計学教室．統計学入門（基礎統計学I）．東京大学出版会 1991
・日本統計学会．日本統計学会公式認定 統計検定 準1級対応 統計学実践ワークブック．学術図書出版社 2020
・mJOHNSNOW．「専門家と学ぶ！はじめの一歩の因果推論 vol.10 Causal Inference What If Chapter 10: Random Variability」発表スライド

参考図書：『Causal Inference: What If』
Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。
mJOHNSNOWでは、こちらの書籍を用いて輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。

そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。

mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する

  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

• vol.15：測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める -

• vol.16：ランダム誤差を徹底解説 -研究結果は「運」で歪むのか？（本記事）