【疫学専門家監修】操作変数を徹底解説 - 「病院までの距離」で交絡因子に対処せよ 　ゼロから学ぶ因果推論 vol.19

シリーズ紹介｜ゼロから学ぶ因果推論

「医学研究は難しい」、きっと多くの方がそう感じているでしょう。

因果推論は、そんな複雑怪奇な医学研究にスッと一本の軸を通してくれる、まさに医学研究の原理原則とも言える学問です。

因果推論を学ぶことで、複雑に散らばっていた知識の断片が見事なまでに因果推論という幹へと体系立てられていきます。そしてきっと「論文、読めるようになってきたかも」、そんな気持ちになれるはず。

「ゼロから学ぶ因果推論」シリーズは、疫学専門家の監修のもとで「はじめて学ぶ人の気持ち」に寄り添い、具体例や図解を使用して「日本でいちばんわかりやすい因果推論の解説」を目指しました。あなたの歩幅で一歩ずつ。ゼロからの学びをはじめしょう。

はじめに

この記事では、操作変数 （Instrumental Variable）について解説します。

因果推論によって「ある介入による、アウトカムに対する因果効果」を調べたい時、避けて通れないのが交絡の問題です。

これまでの解説記事では、交絡に対する最も強力な解決策がランダム化比較試験（RCT）であることをこれまでに解説してきました。しかし、医療や公衆衛生の現場では、倫理的な理由や膨大なコストと労力から、RCTが難しい状況も少なくありません。

そこで登場するのが操作変数法です。

操作変数法は、観察研究において 「未測定交絡に対処して因果効果を推定したい」 というときに用いられる、強力なアプローチです。

本記事では、操作変数の基本的な考え方について、初学者にも理解しやすい形で解説していきます。

mMEDICI Library | ひらけ、叡智の扉

叡智の扉を、全ての人が開けるように——。

学びは、限られた豊かな人々だけの特権ではありません。

経済的困難に直面する人、地方で学習資源に恵まれない人、家事や育児・仕事に追われる人。

mMEDICI Libraryではそんな人々にこそ、最高の学びを届けるため、研究・キャリア・学習・受験のあらゆるテーマでパブリックヘルスの叡智を集めました。

隙間時間にスマホひとつで、誰もが「一流の知」に触れることを叶えていきます。

「ここを開けば、誰しもが悩みを解決できる」、そんなメディアを目指します。

この記事のまとめ

この記事を読むと分かること

• 操作変数の概要

• 操作変数の具体例

• 操作変数推定量の考え方

この記事は誰に向けて書かれているか

• 因果推論の勉強をはじめた初学者

• 操作変数の概要について学びたい方

• 操作変数で交絡調整を実践したい方

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

• vol.15：測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める -

• vol.16：ランダム誤差を徹底解説 - 研究結果は「運」で歪むのか？ -

• vol.17：傾向スコアを徹底解説 - 「治療を受ける確率」で交絡に対処せよ！

• vol.18：媒介分析を徹底解説 - 治療効果のメカニズムを解き明かせ

• vol.19：操作変数を徹底解説 - 「病院までの距離」で交絡因子に対処せよ（本記事）

執筆者の紹介

氏名：氏名：奥山拓郎
所属：株式会社データック
看護大学卒業後、埼玉県の急性期病院にて循環器・心臓血管外科病棟および CCU を担当しました。臨床での経験を通じ、発症前から人々の健康を支える公衆衛生の重要性を感じ、MPHを卒業。現在は、株式会社データックにて、リアルワールドデータを用いて、製薬企業や医療機関の研究支援を行っている。

編集者

氏名：菊池祐介
所属：mMEDICI株式会社
専門性：作業療法学修士。首都大学東京（現東京都立大学）・東京都立大学大学院を卒業後、病院勤務を経て専門学校・私立大学にて作業療法教育、地域共生社会の醸成に向けたリハビリテーション専門職の支援に関する研究に従事。現在は心身の健康とその人らしさの実現に向け、保険内外でのクライアント支援を展開している。作業療法の社会的意義向上を信念に、mMEDICI株式会社に参画。

監修者

氏名：廣瀬直紀
所属：mMEDICI株式会社
専門性：保健学博士・公衆衛生学修士。東京大学・東京大学大学院を卒業後、外資系製薬企業の日本・グローバルにおいて疫学専門家として薬剤疫学・リアルワールドデータ研究に従事。その後、全ての人がアクセス可能な一流の知のプラットフォームを作り、「知に繁栄を、辺野に豊穣を」実現すべく、mMEDICI株式会社を創業。

１. 操作変数とは？

操作変数とは、とても大まかに説明すると「交絡因子に対処し、公平な比較を実現するための手法」の一つです。特に、「未測定交絡」という問題に対する強力な対処法として発展してきた手法です。

操作変数について詳しく理解するためには、まずは「交絡因子」と「未測定交絡」という概念を掴んでおくことが大切ですので、早速一つ一つ確認していきましょう。

交絡因子と「未測定交絡」という難題 

因果推論で最も重要で、かつ最も悩ましい問題の一つが「交絡因子」の存在です。

 交絡因子とは、曝露（または介入）とアウトカムの両方に影響を与える第三の変数であり、適切に調整しないと因果効果の推定が歪められる原因になります。

たとえば、「朝ごはんを食べる子は成績が良い」。よく聞く話ですが、本当にパンやご飯が直接成績を上げているのでしょうか？ここで疑うべきは、背後にある「家庭環境」です。規則正しい生活や親の教育への意識が、朝食と学力の両方に影響している可能性があります。

曝露（X）：朝食を食べるアウトカム（Y）：学力が高い交絡因子（C）：親の教育意識

上記のDAGのように「親の教育意識（ C ）」を通じて、「朝食（ X ）」と「学力（ Y ）」の間に「見せかけの関連」が生じる構造を「交絡」と呼びます。そしてこの「交絡」を引き起こす因子Cを「交絡因子」と呼びます。

交絡についてはこちらの記事で詳しく解説しています。
【疫学専門家監修】交絡を徹底解説 - 結果を歪める、因果推論の最重要課題

このように「曝露（朝食を毎日食べる）」と「アウトカム（学力）」の両方に影響を与える共通の原因が存在すると、本来は直接的な因果関係ではないのに、まるで関係があるように見えてしまうことがあります。そのため、観察研究における因果推論をする際には交絡因子を調整する必要があります。

しかし、観察研究では交絡因子が「未測定（unmeasured）」であったり、測定することが困難なことで、調整すること自体が困難であることがあります。

このような交絡因子を「未測定交絡（Unmeasured Confounding）」と呼びます。

未測定交絡があっても因果効果を推定できる？

傾向スコア法（PS）や逆確率重み付け（IPW）法といった一般的な交絡調整の手法は、「測定された交絡因子」を調整する強力なツールですが、その妥当性は「主要な交絡因子が全て測定されている（＝未測定交絡がない）」という、検証することが困難な仮定に依存しています 。

傾向スコア（PS）の基本解説はこちら
【疫学専門家監修】傾向スコアを徹底解説 - 「治療を受ける確率」で交絡に対処せよ！

IPW（逆確率重み付け）の基本解説はこちら
【疫学専門家監修】逆確率重み付け（Inverse Probability Weighting）を徹底解説 - 交絡調整の基本をわかりやすく図解

それでは、この「未測定交絡」の存在が強く疑われる状況においては、因果効果の推定を諦めなければならないのでしょうか？


操作変数（Instrumental Variable, IV）法は、まさにこの「未測定交絡」が存在する状況下で因果効果を推論するための強力な手法として注目されているアプローチです。

次の章からは、操作変数の基本について一つ一つ学んでいきましょう。

２. 操作変数とは

操作変数（IV）とは、「曝露に影響を与えるが、アウトカムには直接影響を与えず、未測定交絡とも関連しない変数」を指します。このような操作変数はしばしば記号で（ Z ）と表記されます。

操作変数の直感的なイメージとしては、「曝露の割り当てをくじ引きで決める」ような性質の変数です。


例えば、くじ引きで奇数を引いた人は「治療あり」、偶数を引いた人は「治療なし」といったように割り当てた時、くじ引きは治療の有無、つまり「暴露に影響を与えている」ことになります。

一方で、「くじで奇数を引く人ほど死亡率が高い」といった関連は考えにくく、つまりくじ引きの結果は「アウトカムには直接影響しない」変数でもあります。


このように、操作変数とは研究者が恣意的に割り当てたものではなく、くじ引きのように「ランダム」に割り当てたかのように振る舞う変数のことを指します。


くじ引きの他にも、曝露に影響を与えるが、アウトカムに直接は影響しない変数について考えてみましょう。

例えば、経済学や政策評価において、「天候（雨量）」も、古典的な操作変数です。「雨」は人間の意思でコントロールできず、地域や時期によってランダムに発生するため、「自然実験」のような状況を作り出すことができるからです。

自然実験とは
研究者が“実験”をしなくても、社会で“たまたま起きた出来事”が実験のような比較を可能にしてくれる状況のことです。例えば、ある地域だけ早い時期にワクチン接種が始まったときに、まだ接種が始まっていない地域との違いを利用して、ワクチンの効果を調べるといったケースが自然実験に当たります。

ここまでの説明を聞いてピンときた方も多いかと思いますが、この“ランダムに発生する事象”を上手く利用することで、医学研究の「ランダム化比較試験（RCT）」に似た状況を作り出すことができます。

例えば、RCTでは研究者が「サイコロ」を振って治療を割り付けますが、操作変数法では「自然界にある偶然（病院との距離や日付など）」がサイコロの代わりになります。（反対に、RCTにおける無作為割付は、“理想的な操作変数”と捉えることもできます。）

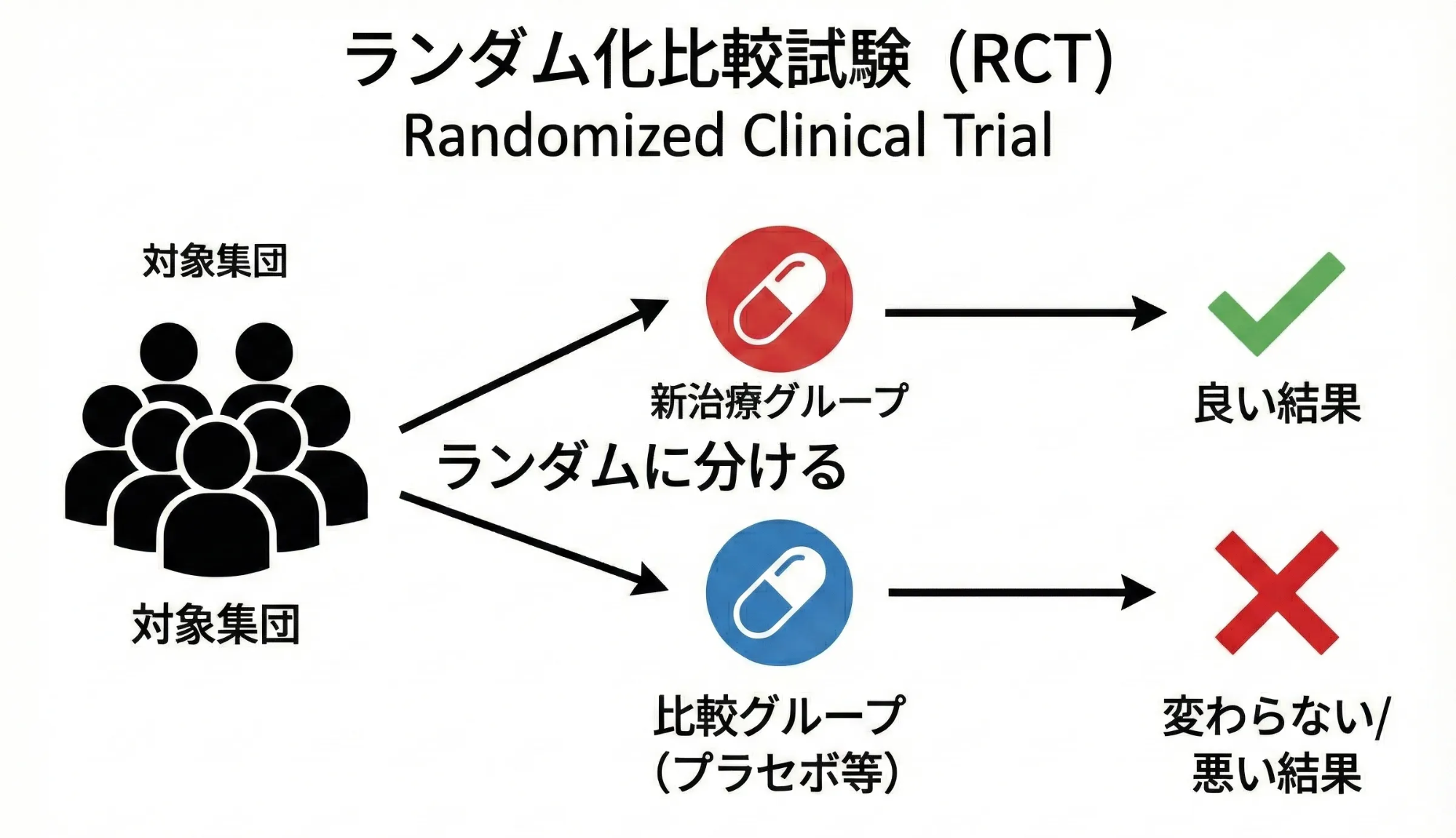
ランダム化による交絡調整についてはこちらの記事をご覧ください
【疫学専門家監修】Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

つまり、操作変数法は、観察データの中で、擬似的にRCTのランダム化を再現しようと試みている手法なのです。

医療分野における操作変数の代表例として、病院や地域ごとの診療方針・処方習慣、医師個人の処方傾向、あるいは専門医療施設までの距離などが挙げられます。

ここでは、二つの研究の実例をもとに操作変数への理解を深めてみましょう。

事例１．操作変数として「治療への物理的な距離」を利用したアプローチ

【参考論文】
McClellan M, McNeil BJ, Newhouse JP. Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? Analysis using instrumental variables. JAMA. 1994 Sep 21;272(11):859-66. PMID: 8078163.

これは、急性心筋梗塞に対する積極的治療（カテーテル検査やステント留置術など）が、保存的治療（薬のみ）に比べて死亡率を下げるかどうかを検証した有名な研究です。

この検証における課題は、医師が「積極的治療に耐えられる体力がある人」を選んで手術を行ったり、逆に「高齢で衰弱している人」には薬のみを選択したりする傾向があることでした。

そのため、単純比較では「積極的治療のおかげ」なのか「もともとの重症度や体力の差」なのか区別がつかない状況だと想定できます。

そこで研究者たちは、患者の重症度ではなく、「患者の自宅から、カテーテル治療ができる専門病院までの距離」を操作変数として利用しました。

自宅の近くにたまたま「専門病院がある人」はカテーテル治療を受けやすく、「専門病院が遠い人」は時間の制約からカテーテル治療を受けにくい傾向があります。つまり、「専門病院までの距離」は、「暴露に影響を与える変数」と言えます。

一方で、心筋梗塞は突然起こるため、「どこに住んでいるか」が発作の重症度と関連することはなく、つまり「専門病院までの距離」は「アウトカムには直接影響しない変数」でもあります。

つまり、「専門病院までの距離」という要素をRCTにおけるサイコロのように利用することで、「暴露（カテーテル治療を受けるかどうか）」が、擬似的にランダム化された状態を作り出し、公平な比較を可能にしたのです。

事例２．操作変数として「医師ごとの診療方針・処方習慣（Surgeon's Preference）」を利用したアプローチ

【参考論文】
Schneeweiss S, Seeger JD, Landon J, Walker AM. Aprotinin during coronary-artery bypass grafting and risk of death. N Engl J Med. 2008 Feb 21;358(8):771-83. doi: 10.1056/NEJMoa0707571. PMID: 18287600.

先行研究に、心臓手術の止血薬「アプロチニン」は死亡率を上げるか？を明らかにしたものがあります。

研究者らは、医師が「重症で出血しやすい患者」や「再手術の患者」にこの薬を使う傾向があるため、単純比較では「薬のせい」か「重症度のせい」か区別できないという交絡の壁に直面しました。

そこで、患者個人の臨床データではなく、「担当した外科医が普段、どのくらいこの薬を使う方針か」を操作変数として利用しました 。

実際のデータにおいて、「ほぼ全ての患者（90%以上）にアプロチニンを使う医師」もいれば、「ほとんど使わない（10%以下）医師」も存在しました 。


患者さんがどの外科医の手術を受けるかは、患者が薬剤の好みで執刀医を選ぶことはないため、患者の重症度やリスク要因とは関係なく、病院のスケジュールや巡り合わせといった「運」で決まります。

つまり、「担当医の好み」がくじ引きのような役割を果たすことで、曝露（薬剤の使用）が擬似的にランダム化された状態で比較が可能になったのです 。

３．操作変数が成立する３条件

この操作変数（IV）が成り立つには以下の三つの条件を満たしていることが必要になります。

• 関連性（The relevance assumption）：操作変数は曝露に十分な影響を与える

• 排除制約（The exclusion restriction）：操作変数はアウトカムに直接影響を与えない

• 独立性（The exchangeability assumptio）：操作変数は未測定交絡と関連しない

例えば、先程の「治療への物理的な距離」を利用した先行研究では、患者の医療施設までの距離を操作変数（ Z ）とし、積極的治療（ X ）が死亡率（ Y ）を下げるかどうかを調べていました。この操作変数の三つの条件は次のようになります。

関連性（The relevance assumption）
この条件は、「患者の医療施設までの距離（ Z ）が積極的治療の受療（ X ）に影響を与えること」を必要とします。
著者らは、積極的治療が可能な病院が、最寄りの病院よりも「かなり遠い」場合（Zが大きい場合）、患者や救急隊は時間的制約から、積極的治療を諦めて最寄りの病院を選ぶ可能性が高まるという仮定をしました


排除制約（The exclusion restriction）
この条件は、「患者の医療施設までの距離（ Z ）が、積極的治療（ X ）という経路以外を通って、死亡率（ Y ）に直接影響を与えないこと」を必要とします。
著者らはカテーテル病院まで「あと10マイル遠い」という事実自体が、患者の予後を直接悪化させる経路はない、という仮定をしました。


独立性（The exchangeability assumption）
最後に、この条件は、「患者の医療施設までの距離（ Z ）が、未測定交絡因子（ U ）と関連しないこと」を必要とします。
著者らは患者がどこに住んでいるかは、多くの場合、急性心筋梗塞の重症度などの未測定交絡とは無関係とみなせるという仮定をしました。

４．操作変数推定の考え方

操作変数の推定量は、「曝露に対するIVの効果」と、「アウトカムに対するIVの効果」の比から計算することができます。
※「均質性の仮定」「単調性の仮定」（次の章で詳細を解説）を満たす場合

そして、この操作変数の推定量は、集団平均因果効果（Average Treatment Effect, ATE）を推定します。

平均因果効果についてはこちらの記事で解説しています。
【疫学専門家監修】因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？

この式が何を示しているか、先程の「操作変数として“病院までの距離”を利用した、急性心筋梗塞に対する積極的治療」の例とDAGによるイメージで考えてみましょう。

① 距離の違い（ Z ）は、積極的治療（ X ）だけに影響する
② 距離の違い（ Z ）による死亡率（ Y ）の変化は、積極的治療（ X ）を介したものだけである
③ その効果を「距離の違いが与えた積極的治療への効果」で割ると、積極的治療が死亡率に与える因果効果がわかる

つまり、距離による死亡率の変化 ÷ 距離による積極的治療の変化 ＝ 積極的治療による死亡率の変化 を求めていることになります


ただし、上記の「操作変数の推定量」は直感的でわかりやすいイメージですが、実際には、変数が連続的（"あり・なし”ではなく、0,1,2,3...という連続した値をとる変数）であったり、未測定交絡が存在したりすることで、「曝露（ X ）の変動の中には、 “操作変数（ Z ）によって説明される部分” と “未測定交絡で説明される部分” の2つが混ざっている」という問題が生じます。

曝露（ X ）の変動 = （操作変数が作った変動） + （未測定交絡が作った変動）

そのため、 操作変数（ Z ） によって説明される曝露（ X ）の変動だけを取り出して、因果効果を推定する必要があります。

こうした状況で用いられるのが「二段階最小二乗法（Two-Stage Least Squares, 2SLS）」です。


少し発展的な手法になるため、ここでは詳細な説明は割愛して概要のみをご紹介します。

まず、2SLSは、回帰モデルという統計手法を使用することで、曝露（ X ）の全変動のうち、操作変数（ Z ）のみによって説明される暴露の変動の大きさ（ X^ ）だけを推定ことができます。すなわち、X^ は未測定交絡（U）の影響を除外した暴露の変動の値となります。

続いて、この回帰モデルから推定された X^ を変数に組み入れた回帰モデルを用いて、X^ がアウトカム（Y）にどのくらい影響を与えるかを推定します。

2SLSはこのステップによって、未測定交絡（U）の影響を除外し、操作変数（Z） によって説明されただけの曝露の影響（ X ^）を取り出して、因果効果を推定することができます。

５．均一性（homogeneity）と単調性（monotonicity）

「３．操作変数が成立する３条件」で解説した３条件は、操作変数の「必要条件」になります。

つまり、例えこれらの条件が満たされたとしても、「４．操作変数推定の考え方」で導出された操作変数の推定量が、私たちが知りたい「因果効果」と一致するためには、均一性（homogeneity）という仮定が必要となります。

均一性（homogeneity）

均一性（homogeneity）とは、「治療効果が全ての人で同じなら、操作変数推定は母集団平均因果効果を推定できる」という仮定になります。

この説明だけを聞いても「難しくてよくわからない...」と感じられるかと思いますので、具体例を用いて考えてみましょう。


先述の事例「操作変数として“病院までの距離”を利用した、急性心筋梗塞に対する積極的治療」の場合で考えてみると、カテーテルなど積極的治療の効果（死亡率の改善）が、「70歳の人にも、糖尿病がある人にも、重症者にも、軽症者にも、どのような患者においても同じ」という仮定になります。

もしこの「均一性」の仮定が三つの条件に加えて成立するならば、操作変数の推定量は、集団平均因果効果の推定量となります 。

しかし、医療分野において、「治療効果がすべての人で全く同じ」などという仮定は、ほとんど成立しない非現実的な仮定になります。

そこで登場するのが、単調性（monotonicity）という仮定です。

単調性（monotonicity）

単調性（monotonicity）は、「効果の均一性」という強すぎる仮定を緩和するために導入された、より現実的な、代替的な仮定です。

単調性とは、「操作変数によって“治療を受けやすくなる人”はいても、逆に“受けにくくなる人”はいない」という仮定になります。

先程の先行研究の例にすると、「近くにカテーテルを積極的に行う病院がある地域に住んでいるから、カテーテル治療を受けやすい」や、反対に「近くにそういった病院がない地域に住んでいるから、治療を受けにくい」という方向で働きますが、「近くにカテーテルを積極的に行う病院があるのに、治療を受けない」という人は存在しないという仮定になります。


この仮定が成り立つことで、操作変数推定量は「LATE（Local Average Treatment Effect：局所平均治療効果）」と呼ばれる、Compliers（従順者）集団における平均因果効果の一致推定量を推定できます 。

つまり、集団全体の中でも、単調整の仮定に従う人（＝ 従順な人）における効果を推定していると解釈できるのです。

この単調性の仮定を理解するために、操作変数（ Z ）によって治療がどのように変化するかで人々を四つのタイプに分類します。

単調性とは この“Defier（逆らう人）がいない” という仮定になります。

「４．操作変数推定の考え方」の操作変数推定量では、この単調性の過程に従い、Complier だけの平均因果効果、「LATE（Local Average Treatment Effect：局所平均治療効果）」を推定していたことになります。

６．操作変数の強みと限界

操作変数法の最大の魅力は、「未測定交絡（Unmeasured Confounding）」を調整できる点になります。

傾向スコア（PS）法や逆確率重み付け（IPW）法を含む、観察研究で一般的に用いられる調整手法は、「“測定された共変量”によって、交絡が十分に制御されていること」という仮定に依存しています 。

そのため、PSとIPWは、観測された交絡因子を調整させるための洗練された手法でありますが、測定できていない交絡因子（Unmeasured Confounders）によるバイアスは除去できていないという弱点があります。

一方で、操作変数は、上記で説明してきたようにこの「未測定交絡がない」という仮定が保証されない状況でも、因果効果を推定できる手段です。

ただし、このような万能にみえる操作変数でも弱点があります。それは三つの条件を同時に満たす変数を現実世界で見つけることは、極めて困難なことです。

特に、「排除制約」と「独立性」は検証不可能とされ、常に批判の対象となっています。（そもそも“未測定”の交絡と操作変数との関連性を検証することが困難であることは、想像に難くありませんね？）

また、これらの条件から少しでも逸脱した場合、大きなバイアスが生じ得ます。例えば、条件「関連性」において、操作変数（ Z ）と暴露（ X ）との関連が弱い（Weak Instrument ）の場合などには、推定値が不安定になるといった課題も包含しています。

７．まとめ

操作変数は「最後の切り札」的な方法

操作変数法は、観察研究における最大の難敵である「未測定交絡」に立ち向かうための、理論上、非常に強力な手法の一つです 。

しかし、三つの条件を満たす「妥当な操作変数」を検証することが難しいことが課題でもあります。

そのため、操作変数法は、安易に適用されるべき方法ではなく、強力な未測定交絡の存在が強く疑われ、かつ、３条件を理論的に強く擁護できる「非常に良い」操作変数の候補が見つかった場合にのみ用いられるべき、「最後の切り札」的な手法です。

そのため、操作変数を用いた論文を読む際には、推定された因果効果の数値そのものよりも、その推定値の「妥当性」を支える３条件が妥当か必ず考える必要があります。

因果推論の文脈において、三つの厳格な条件を満たす「良い操作変数」を見つけ出すこと、そしてその妥当性を理論的に検証すること自体が、因果推論における研究の質を高めることにつながるのです。

参考文献

Walker V, Sanderson E, Levin MG, Damraurer SM, Feeney T, Davies NM. Reading and conducting instrumental variable studies: guide, glossary, and checklist. BMJ. 2024 Oct 14;387:e078093. doi: 10.1136/bmj-2023-078093. PMID: 39401839; PMCID: PMC11472180.

McClellan M, McNeil BJ, Newhouse JP. Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? Analysis using instrumentalvariables. JAMA. 1994 Sep 21;272(11):859-66. PMID: 8078163.

Schneeweiss S, Seeger JD, Landon J, Walker AM. Aprotinin during coronary-artery bypass grafting and risk of death. N Engl J Med. 2008 Feb 21;358(8):771-83. doi: 10.1056/NEJMoa0707571. PMID: 18287600.

Matthay EC, Smith ML, Glymour MM, White JS, Gradus JL. Opportunities and challenges in using instrumental variables to study causal effects in nonrandomized stress and trauma research. Psychol Trauma. 2023 Sep;15(6):917-929. doi: 10.1037/tra0001370. Epub 2022 Oct 13. PMID: 36227293; PMCID: PMC10097832.

参考図書：『Causal Inference: What If』
Causal Inference: What Ifとはハーバード大学のSPHで教鞭をとるMiguel Hernan氏とJames Robins氏によって執筆された因果推論の金字塔的書籍です。
医学研究オンラインスクールmJOHNSNOWでは、こちらの書籍を題材として輪読会を行い因果推論をゼロから学んでいます。

因果推論を学ぶならオンラインスクールmJOHNSNOW

この記事を読み、「もっと因果推論を学びたい」と思われた方もいらっしゃるでしょう。

そんな方には弊社が運営するオンラインスクールmJOHNSNOWがお勧めです。

mJOHNSNOWはスペシャリストが運営する臨床研究・パブリックヘルスに特化した日本最大規模の入会審査制オンラインスクールです。運営・フェローの専門は疫学、生物統計学、リアルワールドデータ、臨床、企業など多岐に渡り、東大、京大、ハーバード、ジョンスホプキンス、LSHTMなど世界のトップスクールの卒業生も集まっています。

本日解説した因果推論の講義に加えて、みなさんの専門性を伸ばすためのコンテンツが目白押しです！

・スペシャリスト監修の臨床研究・パブリックヘルスの講義が毎月7つ以上開催
・過去の講義が全てオンデマンド動画化されたレポジトリー
・スクール内のスペシャリストに学術・キャリアの相談ができるチャットコンサル
・フェローが自由に設立して学べるピアグループ（ex. RWDピア）
・24時間利用可能なオンライン自習室

「パブリックヘルスを、生き様に」をミッションに、『初心者が、自立して臨床研究・パブリックヘルスの実践者になる』ことを目指して学んでいます。初心者の方も大勢所属しており、次のような手厚いサポートがあるので安心してご参加ください！

・オンデマンド動画があるから納得するまで何回でも、いつでも学び直せる
・チャットコンサルで質問すれば24時間以内にスペシャリストから複数の回答が
・初心者専用の「優しいピアグループ」で助け合い、スペシャリストが”講義の解説”講義を毎月開催

詳細を見る ｜ 無料体験に申し込む

【YouTubeラジオコンテンツ　耳から学ぶシリーズ】

YouTubeラジオコンテンツ「耳から学ぶシリーズ」は、仕事や育児で忙しい人が10分のスキマ時間に“ながら聞き”で学べる音声コンテンツです。

すべてのコンテンツを疫学専門家が監修し、完全無料で毎日投稿していきますので、ぜひチャンネル登録してお待ちください。

シリーズ一覧

• 耳から学ぶ 因果推論

• 耳から学ぶ 医療職・研究者のための生成AI活用術

• 耳から学ぶ 医学研究デザイン

• 耳から学ぶ 生物統計

因果推論シリーズ

• vol.1：因果推論の出発点 - 因果と関連の違いとは？ -

• vol.2：因果効果の基本を徹底解説 - Individual Causal Effect（個人因果効果）とAverage Causal Effect（平均因果効果）の違いとは？ -

• vol.3：初心者のためのTarget Trial Emulation（TTE）
  - Part 1 ; ETAFOCAフレームワークについて
  - Part 2 ; 三つの時点で考えるバイアスとその対処法
  - Part 3 ; 論文の実例で理解を深めるTTE

• vol.4：Exchangeability（交換可能性）を徹底解説 - Randomization（ランダム化）が実現する因果推論の必須条件 -

• vol.5：Standardization（標準化）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.6：Inverse Probability Weighting（逆確率重み付け）を徹底解説 - 交絡調整の基本をわかりやすく図解 -

• vol.7：Consistency（一致性）を徹底解説 - 観測データと反事実アウトカムを一致させよ -

• vol.8：Positivity（正値性）を徹底解説 - 因果推論の落とし穴を回避せよ -

• vol.9：Immortal time biasを徹底解説 - 臨床研究に潜む「不死の時間」の罠 -

• vol.10：効果修飾を徹底解説 - 私たちは「どの集団における」効果を見ているのか？ -

• vol.11：交互作用を徹底解説 - 複数の介入による相乗効果 -

• vol.12：DAGを徹底解説

  - 基礎編；因果推論の必須ツールで交絡因子を可視化する
  - 応用編；調整してはならない？コライダーと媒介変数の落とし穴

• vol.13：交絡を徹底解説 - 結果を歪める、因果推論の最重要課題 -

• vol.14：選択バイアスを徹底解説 - 消えた患者が結果を歪める？- 

• vol.15：測定バイアスを徹底解説 - ズレたメジャーが、結果を歪める -

• vol.16：ランダム誤差を徹底解説 - 研究結果は「運」で歪むのか？ -

• vol.17：傾向スコアを徹底解説 - 「治療を受ける確率」で交絡に対処せよ！

• vol.18：媒介分析を徹底解説 - 治療効果のメカニズムを解き明かせ

• vol.19：操作変数を徹底解説 - 「病院までの距離」で交絡因子に対処せよ（本記事）